
| 5 |
| 9 |
| 5 |
| 9 |
| 1 |
| 2 |
| 5 |
| 9 |
| 2 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 6 |
| 5 |
| 6 |
| 1 |
| 3 |
| 5 |
| 6 |
| 5 |
| 9 |
| 1 |
| 2 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
| 1 |
| 3 |
Pn+1-
| ||
Pn-
|
| 1 |
| 2 |
| 5 |
| 9 |
| 5 |
| 9 |
| 1 |
| 3 |
| 5 |
| 9 |
| 2 |
| 9 |
| 1 |
| 2 |
| 5 |
| 9 |
| 2 |
| 9 |
| 1 |
| 2 |
| 5 |
| 9 |
| (-1)n |
| 9•2n-2 |
| 5 |
| 9 |
| 5 |
| 9 |
| 2 |
| 9 |
| 1 |
| 2 |
| Snk+1→(n+1)k |
| S(n-1)k+1→nk |
| a1qnk(1+q+…+qk-1) |
| a1q(n-1)k(1+q+…+qk-1) |
-
| ||||
1+
|
| 4 |
| 27 |
| 1 |
| 2 |
| S1→k(1-qkn) |
| 1-qk |
-
| ||||||
1-(-
|
| 4 |
| 27 |
| 1 |
| 2 |
-
| ||||
1+
|
| 4 |
| 27 |
| 1 |
| 2 |


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
| 5 |
| 9 |
| 5 |
| 9 |
| 1 |
| 2 |
| 5 |
| 9 |
查看答案和解析>>
科目:高中数学 来源:2007年广东省湛江市高考数学二模试卷(理科)(解析版) 题型:解答题
 ,
, ),斜率为
),斜率为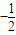 的直线上;
的直线上; }从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.查看答案和解析>>
科目:高中数学 来源:模拟题 题型:解答题
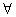 n∈N*,点(Pn,Pn+1)恒在过定点
n∈N*,点(Pn,Pn+1)恒在过定点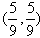 斜率为-
斜率为-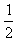 的直线上;
的直线上;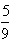 }从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…S(n-1)k+1→nk的前n项和Tn。
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…S(n-1)k+1→nk的前n项和Tn。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com