
已知椭圆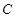 :
: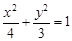 的左、右焦点分别为
的左、右焦点分别为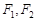 ,椭圆
,椭圆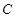 上点
上点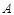 满足
满足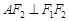 . 若点
. 若点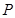 是椭圆
是椭圆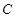 上的动点,则
上的动点,则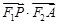 的最大值为( )
的最大值为( )
A.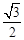 | B.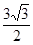 | C.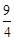 | D.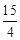 |
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:单选题
已知双曲线 的左焦点为F1,左、右顶点分别为A1、A2,P为双曲线上任意一点,则分别以线段PF1,A1A2为直径的两个圆的位置关系为( )
的左焦点为F1,左、右顶点分别为A1、A2,P为双曲线上任意一点,则分别以线段PF1,A1A2为直径的两个圆的位置关系为( )
| A.相交 | B.相切 | C.相离 | D.以上情况都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知等边△ABC中,D、E分别是CA、CB的中点,以A、B为焦点且过D、E的椭圆和双曲线的离心率分别为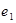 、
、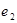 ,则下列关于
,则下列关于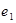 、
、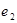 的关系式不正确的是( )
的关系式不正确的是( )
A.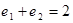 B.
B.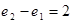 C.
C.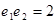 D.
D.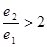
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com