练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．A城市的出租车计价方式为：若行程不超过3千米，则按“起步价”10元计价；若行程超过3千米，则之后2千米以内的行程按“里程价”计价，单价为1.5元/千米；若行程超过5千米，则之后的行程按“返程价”计价，单价为2.5元/千米．设某人的出行行程为x千米，现有两种乘车方案：①乘坐一辆出租车；②每5千米换乘一辆出租车．
    （Ⅰ）分别写出两种乘车方案计价的函数关系式；
    （Ⅱ）对不同的出行行程，①②两种方案中哪种方案的价格较低？请说明理由．

    分析 （Ⅰ）根据两种乘车方案：①乘坐一辆出租车；②每5千米换乘一辆出租车，分别写出两种乘车方案计价的函数关系式；
    （Ⅱ）分类讨论，作差，即可得出对不同的出行行程，①②两种方案中哪种方案的价格较低．

    解答 解：（Ⅰ）方案①计价的函数为f（x），方案②计价的函数为g（x），
    则f（x）=$\left\{\begin{array}{l}{10，0＜x≤3}\\{10+1.5（x-3），3＜x≤5}\\{13+2.5（x-5），x＞5}\end{array}\right.$；
    g（x）=$\left\{\begin{array}{l}{13k+10，5k＜x≤5k+3（k∈N）}\\{13k+10+1.5（x-5k-3），5k+3＜x≤5k+5（k∈N）}\end{array}\right.$；
    （Ⅱ）当0＜x≤5时，f（x）=g（x），
    x＞5时，f（x）＜g（x）即方案①的价格比方案②的价格低，
    理由如下：
    x∈（5k，5k+3）（k∈N），f（x）-g（x）=2.5x-13k-9.5≤-0.5k-2＜0；
    x∈（5k+3，5k+5）（k∈N），f（x）-g（x）=x-5.5k-5≤-0.5k＜0．

    点评 本题考查了分段函数在实际问题中的应用，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．三棱锥SABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为（　　）
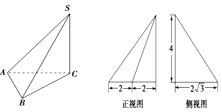
    A．4$\sqrt{2}$B．$\sqrt{19}$C．$\sqrt{20}$D．$4\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知F1，F2为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{16}$=1（a＞0）的左右焦点，点A在双曲线的右支上，点P（7，2）是平面内一定点，若对任意实数m，直线4x+3y+m=0与双曲线C至多有一个公共点，则|AP|+|AF2|的最小值为（　　）
    A．2$\sqrt{37}$-6B．10-3$\sqrt{5}$C．8-$\sqrt{37}$D．2$\sqrt{5}$-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．根据下列条件，求双曲线的标准方程．
    （1）与已知双曲线x2-4y2=4有共同渐近线且经过点（2，2）；
    （2）渐近线方程为y=±$\frac{1}{2}$x，焦距为10；
    （3）经过两点P（-3，2$\sqrt{7}$）和Q（-6$\sqrt{2}$，-7）；
    （4）双曲线中心在原点，焦点在坐标轴上，离心率为$\sqrt{2}$，且过点（4，-$\sqrt{10}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．集合M={x|x2-x-6≥0}，集合N={x|-3≤x≤1}，则N∩（∁RM）等于（　　）
    A．[-2，1]B．（-2，1]C．[-3，3）D．（-2，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．函数f（x）=loga|x+1|在（-1，0）上是增函数，则f（x）在（-∞，-1）上是（　　）
    A．函数值由负到正且为增函数B．函数值恒为正且为减函数
    C．函数值由正到负且为减函数D．没有单调性

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若${（{X-2}）^5}={a_5}{X^5}+{a_4}{X^4}+{a_3}{X^3}+{a_2}{X^2}+{a_1}X+{a_0}$，则a1+a2+a3+a4+a5=（　　）
    A．-1B．31C．-33D．-31

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．{an}是等差数列，{bn}是等比数列，Tn是{bn}的前n项和，a1=b1=1，且满足$\sqrt{{a_2}+2}+\sqrt{{b_2}-2}=2\sqrt{2}$，当a2+b2取最小值时，
    （1）求Tn；
    （2）Sn是{|an|}的前n项和，求Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．设等比数列{an}的公比q=1，前n项和为Sn，则$\frac{{S}_{4}}{{a}_{2}}$=（　　）
    A．2B．4C．$\frac{15}{2}$D．$\frac{17}{2}$

    查看答案和解析>>

    同步练习册答案