Question

【题目】在△ABC中，(1)已知a＝，b＝，B＝45°，求A、C、c；

(2)已知sin A∶sin B∶sin C＝(＋1)∶(－1)∶，求最大角．

Answer 1

【答案】（1）A＝60°，C＝75°，c＝，或A＝120°，C＝15°，c＝. （2）

【解析】试题分析：（1）由正弦定理求解即可，注意三角形解的个数的讨论；（2）由条件可判断C最大，设出三边，根据余弦定理求解。

试题解析：

(1)由正弦定理及已知条件有＝，

得sin A＝，

∵a>b，

∴A>B＝45°，

∴A＝60°或120°.

①当A＝60°时，C＝180°－45°－60°＝75°，

∴c＝＝＝，

②当A＝120°时，C＝180°－45°－120°＝15°，

∴c＝＝＝.

综上，A＝60°，C＝75°，c＝，或A＝120°，C＝15°，c＝.

(2)根据正弦定理可知a∶b∶c＝sin A∶sin B∶sin C＝(＋1)∶(－1)∶，

设，

由余弦定理的推理得

，

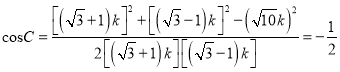又，

∴

∴最大角为C且．