
【题目】对一个量用两种方法分别算一次,由结果相同而构造等式,这种方法称为“算两次”的思想方法.利用这种方法,结合二项式定理,可以得到很多有趣的组合恒等式.
(1)根据恒等式![]() 两边
两边![]() 的系数相同直接写出一个恒等式,其中
的系数相同直接写出一个恒等式,其中![]() ;
;
(2)设![]() ,利用上述恒等式证明:
,利用上述恒等式证明:![]() .
.
科目:高中数学 来源: 题型:
【题目】某地有三家工厂,分别位于矩形ABCD的顶点A,B,及CD的中点P处,已知![]() km,
km,![]() ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
(I)按下列要求写出函数关系式:
①设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
②设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(I)中的一个函数关系式,确定污水处理厂的位置,使三条排水管道总长度最短.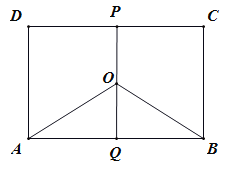
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为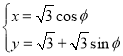 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,点
的交点,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,
的交点,![]() 、
、![]() 均异于原点
均异于原点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
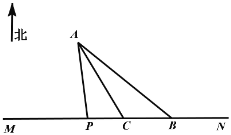
【题目】如图,海岸公路MN的北方有一个小岛A(大小忽略不计)盛产海产品,在公路MN的B处有一个海产品集散中心,点C在B的正西方向10![]() 处,
处,![]() ,
,![]() ,计划开辟一条运输线将小岛的海产品运送到集散中心.现有两种方案:①沿线段AB开辟海上航线:②在海岸公路MN上选一点P建一个码头,先从海上运到码头,再公路MN运送到集散中心.已知海上运输、岸上运输费用分别为400元/
,计划开辟一条运输线将小岛的海产品运送到集散中心.现有两种方案:①沿线段AB开辟海上航线:②在海岸公路MN上选一点P建一个码头,先从海上运到码头,再公路MN运送到集散中心.已知海上运输、岸上运输费用分别为400元/![]() 、200元/
、200元/![]() .
.
(1)求方案①的运输费用;
(2)请确定P点的位置,使得按方案②运送时运输费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济结构调整和方式转变,社会对高质量人才的需求越来越大,因此考研现象在我国不断升温.某大学一学院甲、乙两个本科专业,研究生的报考和录取情况如下表,则
性别 | 甲专业报考人数 | 乙专业报考人数 | 性别 | 甲专业录取率 | 乙专业录取率 | |
男 | 100 | 400 | 男 |
|
| |
女 | 300 | 100 | 女 |
|
|
A.甲专业比乙专业的录取率高B.乙专业比甲专业的录取率高
C.男生比女生的录取率高D.女生比男生的录取率高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() 的周长为12.
的周长为12.
(1)求点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)已知点![]() ,是否存在过点
,是否存在过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
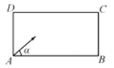
【题目】台球运动已有五、六百年的历史,参与者用球杆在台上击球.若和光线一样,台球在球台上碰到障碍物后也遵从反射定律如图,有一张长方形球台ABCD,![]() ,现从角落A沿角
,现从角落A沿角![]() 的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则
的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com