
【题目】某市开发了一块等腰梯形的菜花风景区![]() (如图).经测量,
(如图).经测量,![]() 长为
长为![]() 百米,
百米,![]() 长为
长为![]() 百米,
百米,![]() 与
与![]() 相距
相距![]() 百米,田地内有一条笔直的小路
百米,田地内有一条笔直的小路![]() (
(![]() 在
在![]() 上,
上,![]() 在
在![]() 上)与
上)与![]() 平行且相距
平行且相距![]() 百米.现准备从风景区入口处
百米.现准备从风景区入口处![]() 出发再修一条笔直的小路
出发再修一条笔直的小路![]() 与
与![]() 交于
交于![]() ,在小路
,在小路![]() 与
与![]() 的交点
的交点![]() 处拟建一座瞭望塔.
处拟建一座瞭望塔.
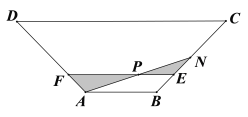
(1)若瞭望塔![]() 恰好建在小路
恰好建在小路![]() 的中点处,求小路
的中点处,求小路![]() 的长;
的长;
(2)两条小路![]() 与
与![]() 将菜花风景区划分为四个区域,若将图中阴影部分规划为观赏区.求观赏区面积
将菜花风景区划分为四个区域,若将图中阴影部分规划为观赏区.求观赏区面积![]() 的最小值.
的最小值.
【答案】(1)![]() 百米;(2)(
百米;(2)(![]() )平方百米.
)平方百米.
【解析】
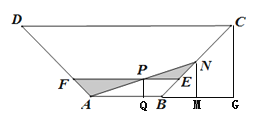
(1)过点P、N、C分别做AB的垂线,垂足分别为Q、M、G,在直角三角形AMN中,结合勾股定理,即可求解;
(2)以直线CD所在直线为![]() 轴,边CD的垂直平分线为
轴,边CD的垂直平分线为![]() 轴建立如图所示的平面直角坐标系,设
轴建立如图所示的平面直角坐标系,设![]() ,得出面积
,得出面积![]() ,结合基本不等式,即可求解.
,结合基本不等式,即可求解.
(1)过点P、N、C分别做AB的垂线,垂足分别为Q、M、G,
因为P是AN的中点,所以![]() ,
,
由已知条件易知![]() 是等腰直角三角形,所以
是等腰直角三角形,所以![]() ,
,
所以![]() ,
,
在直角三角形AMN中,由勾股定理得![]() ,
,
答:小路AN的长为![]() 百米;
百米;
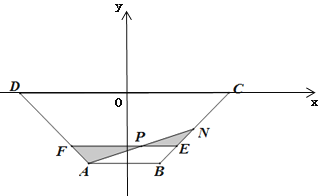
(2)以直线CD所在直线为![]() 轴,边CD的垂直平分线为
轴,边CD的垂直平分线为![]() 轴建立如图所示的平面直角坐标系,
轴建立如图所示的平面直角坐标系,
设![]() ,则直线
,则直线![]() ,
,
联立直线![]() ,得
,得![]() ,
,
所以![]() 的高为
的高为![]() ,
,
所以![]() ,
,
令![]() ,则
,则![]() ,
,
所以当![]() 即
即![]() 时,S的最小值为
时,S的最小值为![]() .
.
答:观赏区面积![]() 的最小值为(
的最小值为(![]() )平方百米.
)平方百米.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率是圆的周长与直径的比值,一般用字母![]() 表示.我们可以通过设计一个试验来估计
表示.我们可以通过设计一个试验来估计![]() 的值:从
的值:从![]() 表示的区域内随机抽取200个实数对
表示的区域内随机抽取200个实数对![]() ,其中x,y两个数能与1构成钝角三角形三边长的数对
,其中x,y两个数能与1构成钝角三角形三边长的数对![]() 共有56个.则用随机模拟的方法估计
共有56个.则用随机模拟的方法估计![]() 的近似值为________.
的近似值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民用天然气实行阶梯价格制度,具体见下表:
阶梯 | 年用气量(立方米) | 价格(元/立方米) |
第一阶梯 | 不超过228的部分 | 3.25 |
第二阶梯 | 超过228而不超过348的部分 | 3.83 |
第三阶梯 | 超过348的部分 | 4.70 |
从该市随机抽取10户(一套住宅为一户)同一年的天然气使用情况,得到统计表如下:
居民用气编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年用气量(立方米) | 95 | 106 | 112 | 161 | 210 | 227 | 256 | 313 | 325 | 457 |
(1)求一户居民年用气费y(元)关于年用气量x(立方米)的函数关系式;
(2)现要在这10户家庭中任意抽取3户,求抽到的年用气量超过228立方米而不超过348立方米的用户数的分布列与数学期望;
(3)若以表中抽到的10户作为样本估计全市居民的年用气情况,现从全市中依次抽取10户,其中恰有k户年用气量不超过228立方米的概率为![]() ,求
,求![]() 取最大值时的值.
取最大值时的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
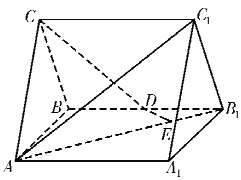
(I)若![]() 为
为![]() 上的一点,且
上的一点,且![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)在(I)的条件下,设异面直线![]() 与
与![]() 所成的角为45°,求直线
所成的角为45°,求直线![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图为国家统计局网站发布的《2018年国民经济和社会发展统计公报》中居民消费价格月度涨跌幅度的折线图(注:同比是今年第![]() 个月与去年第
个月与去年第![]() 个月之比,环比是现在的统计周期和上一个统计周期之比)
个月之比,环比是现在的统计周期和上一个统计周期之比)
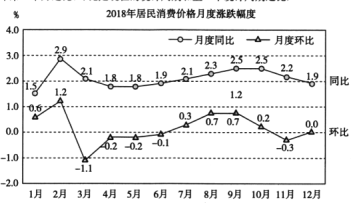
下列说法正确的是( )
①2018年6月CPI环比下降0.1%,同比上涨1.9%
②2018年3月CPI环比下降1.1%,同比上涨2.1%
③2018年2月CPI环比上涨0.6%,同比上涨1.4%
④2018年6月CPI同比涨幅比上月略微扩大1.9个百分点
A.①②B.③④C.①③D.②④.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—5:参数方程选讲]
在直角坐标系xoy中,曲线![]() 的参数方程是
的参数方程是 (t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线
(t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]()
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若两曲线交点为A、B,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点![]() 的动直线
的动直线![]() 与圆
与圆![]() :
: ![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得当
,使得当![]() 变动时,总有直线
变动时,总有直线![]() 的斜率之和为0?若存在,求出
的斜率之和为0?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com