
【题目】甲、乙两位同学学生参加数学竞赛培训,在培训期间他们参加5项预赛,成绩如下:
甲:78 76 74 90 82
乙:90 70 75 85 80
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,从平均数、方差的角度考虑,你认为选派哪位学生参加合适?说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】对一批电子元件进行寿命追踪调查,从这批产品中抽取![]() 个产品(其中
个产品(其中![]() ),得到频率分布直方图如下:
),得到频率分布直方图如下:

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从频率分布直方图估算这批电子元件寿命的平均数、中位数的估计分别是多少?
(Ⅲ)现要从300![]() 400及400
400及400![]() 500这两组中按照分层抽样的方法抽取一个样本容量为36的样本,则在300
500这两组中按照分层抽样的方法抽取一个样本容量为36的样本,则在300![]() 400及400
400及400![]() 500这两组分别抽多少件产品.
500这两组分别抽多少件产品.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)将曲线![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() ,2倍后得到曲线
,2倍后得到曲线![]() ,试写出直线
,试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面五边形![]() 是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,
是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,![]() ,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
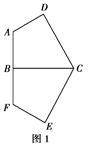
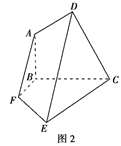
(1)证明:AF∥平面DEC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.”某市交警在该市一交通岗前设点对过往的车辆进行抽查,经过一晚的抽查,共查出酒后驾车者60名,图甲是用酒精测试仪对这60 名酒后驾车者血液中酒精浓度进行检测后依所得结果画出的频率分布直方图.
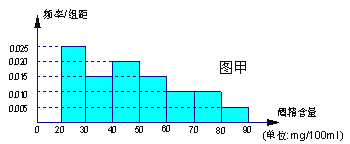
(1)统计方法中,同一组数据常用该组区间的中点值作为代表,图乙的程序框图是对这60名酒后驾车者血液的酒精浓度做进一步的统计,求出图乙输出的S的值,并说明S的统计意义;(图乙中数据![]() 与
与![]() 分别表示图甲中各组的组中值及频率)
分别表示图甲中各组的组中值及频率)

(2)本次行动中,吴、李两位先生都被酒精测试仪测得酒精浓度属于70~90![]() 的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90
的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90![]() 范围的酒后驾车者中随机抽出2人抽血检验,设
范围的酒后驾车者中随机抽出2人抽血检验,设![]() 为吴、李两位先生被抽中的人数,求
为吴、李两位先生被抽中的人数,求![]() 的分布列,并求吴、李两位先生至少有1人被抽中的概率.
的分布列,并求吴、李两位先生至少有1人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宜昌一中江南新校区拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米,设小圆弧所在圆的半径为![]() 米,圆心角
米,圆心角![]() (弧度).
(弧度).
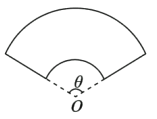
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米,设花坛的面积与装饰总费用之比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com