练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

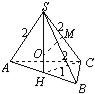
    【题目】已知三棱锥S-ABC的底面是以AB为斜边的等腰直角三角形，SA=SB= SC=2，AB=2，设S、A、B、C四点均在以O为球心的某个球面上。则点O到平面ABC的距离为________________。

    【答案】

    【解析】

    试题根据三棱锥S﹣ABC的底面是以AB为斜边的等腰直角三角形，SA=SB=SC，可得S在面ABC上的射影为AB中点H，SH⊥平面ABC，在面SHC内作SC的垂直平分线MO与SH交于O，则O为SABC的外接球球心，OH为O与平面ABC的距离，由此可得结论．

    解：∵三棱锥S﹣ABC的底面是以AB为斜边的等腰直角三角形，SA=SB=SC，

    ∴S在面ABC上的射影为AB中点H，∴SH⊥平面ABC．

    ∴SH上任意一点到A、B、C的距离相等．

    ∵SH=，CH=1，在面SHC内作SC的垂直平分线MO与SH交于O，则O为SABC的外接球球心．

    ∵SC=2

    ∴SM=1，∠OSM=30°

    ∴SO=，∴OH=，即为O与平面ABC的距离．

    故答案为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝(x－k)ex.

    (1)求f(x)的单调区间；

    (2)求f(x)在区间[0,1]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知极点与直角坐标系原点重合，极轴与x轴的正半轴重合，圆C的极坐标方程为，直线l的参数方程为为参数．

    若，直线l与x轴的交点为M，N是圆C上一动点，求的最小值；

    若直线l被圆C截得的弦长等于圆C的半径，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：x2＝2py（p＞0）的焦点为F，抛物线上一点P的纵坐标为3，且｜PF｜＝4，过M（m，0）作抛物线C的切线MA（斜率不为0），切点为A．

    （1）求抛物线C的方程；

    （2）求证：以FA为直径的圆过点M．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于以，为公共焦点的椭圆和双曲线，设是它们的一个公共点，，分别为它们的离心率.若，则的最大值为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知两个半径不相等的与相交于M、N两点，且、分别与内切于S、T两点。求证：OM⊥MN的充分必要条件是S、N、T三点共线。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数y＝f（x）的定义域为R，并且满足f（x+y）＝f（x）+f（y），f（）＝1，当x＞0时，f（x）＞0．

    （1）求f（0）的值；

    （2）判断函数的奇偶性；

    （3）如果f（x）+f（2+x）＜2，求x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    设平面上向量＝(cosα，sinα) (0°≤α＜360°)，＝(－，)．

    (1)试证：向量与垂直；

    (2)当两个向量与的模相等时，求角α.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义：若两个椭圆的离心率相等，则称两个椭圆是“相似”的．如图，椭圆与椭圆是相似的两个椭圆，并且相交于上下两个顶点，椭圆的长轴长是4，椭圆长轴长是2，点，分别是椭圆的左焦点与右焦点.

    （1）求椭圆，的方程；

    （2）过的直线交椭圆于点，，求面积的最大值.

    查看答案和解析>>

    同步练习册答案