
����Ŀ��ijУ100��ѧ�����п������ijɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ����������ǣ�[50��60����[60��70����[70��80����[80��90����[90��100]�� 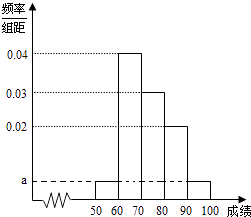
��1����ͼ��a��ֵ��
��2������Ƶ�ʷֲ�ֱ��ͼ��������100��ѧ�����ijɼ���ƽ���֣�
��3������100��ѧ�����ijɼ�ijЩ�����ε�������x������ѧ�ɼ���Ӧ�����ε�������y��֮�������ʾ������ѧ�ɼ���[50��90��֮���������
������ | [50��60�� | [60��70�� | [70��80�� | [80��90�� |
x��y | 1��1 | 2��1 | 3��4 | 4��5 |
���𰸡�
��1���⣺������ã�10��2a+0.02+0.03+0.04��=1�����a=0.005
��2���⣺��100��ѧ�����ijɼ���ƽ����Ϊ��55��0.05+65��0.4+75��0.3+85��0.2+95��0.05=73���֣�
��3���⣺��ѧ�ɼ���[50��60��������Ϊ��100��0.05=5��
��ѧ�ɼ���[60��70��������Ϊ�� ![]() ��
��
��ѧ�ɼ���[70��80��������Ϊ�� ![]() ��
��
��ѧ�ɼ���[80��90��������Ϊ�� ![]() ��
��
������ѧ�ɼ���[50��90��֮�������Ϊ��100��5��20��40��25=10
����������1����Ƶ�ʷֲ�ֱ��ͼ�����ʿ�10��2a+0.02+0.03+0.04��=1���ⷽ�̼��ɵõ�a��ֵ����2����ƽ������Ȩ��ʽ�ɵ�ƽ����Ϊ55��0.05+65��0.4+75��0.3+85��0.2+95��0.05�������������ã���3�����������������ݷֱ�������ѧ�ɼ��ڷ����ε����������������м�ȥ��Щ���ڵ��������ɵó���ѧ�ɼ���[50��90��֮���������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ��������ֵ��
��������ֵ��![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ������
������![]() ���������
���������![]() �����ֵΪ
�����ֵΪ![]() ��֤����
��֤���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��������˵����ȷ���ǣ� ��
��������˵����ȷ���ǣ� ��
A. ��![]() �ϸ���������쳤��ԭ����2���������겻�䣬�ٰѵõ�����������ƽ��
�ϸ���������쳤��ԭ����2���������겻�䣬�ٰѵõ�����������ƽ��![]() ����λ���ȣ��õ�����
����λ���ȣ��õ�����![]()
B. ��![]() �ϸ���������쳤��ԭ����2���������겻�䣬�ٰѵõ�����������ƽ��
�ϸ���������쳤��ԭ����2���������겻�䣬�ٰѵõ�����������ƽ��![]() ����λ���ȣ��õ�����
����λ���ȣ��õ�����![]()
C. ������![]() ����ƽ��
����ƽ��![]() ����λ���ȣ��ٰѵõ��������ϸ�����������̵�ԭ����
����λ���ȣ��ٰѵõ��������ϸ�����������̵�ԭ����![]() �������겻�䣬�õ�����
�������겻�䣬�õ�����![]()
D. ������![]() ����ƽ��
����ƽ��![]() ����λ���ȣ��ٰѵõ��������ϸ�����������̵�ԭ����
����λ���ȣ��ٰѵõ��������ϸ�����������̵�ԭ����![]() �������겻�䣬�õ�����
�������겻�䣬�õ�����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� ![]() =��cos�ȣ�sin�ȣ���
=��cos�ȣ�sin�ȣ��� ![]() =����
=���� ![]() ��
�� ![]() ����
����
��1���� ![]() ��
�� ![]() ���Ҧȡʣ�0���У�����ȣ�
���Ҧȡʣ�0���У�����ȣ�
��2����|3 ![]() +
+ ![]() |=|
|=| ![]() ��3
��3 ![]() |����|
|����| ![]() +
+ ![]() |��ֵ��
|��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͥ��������Ͷ�ʣ����ݳ����������г������Ԥ�⣬Ͷ��ծȯ���ȼ��Ͳ�ƷA��������Ͷ�ʳ����ȣ����ϵ��ͼ1��ʾ��Ͷ�ʹ�Ʊ�ȷ����Ͳ�ƷB��������Ͷ�ʵ�����ƽ���������ȣ����ϵ��ͼ2��ʾ��������Ͷ�ʵ�λ����Ԫ���� 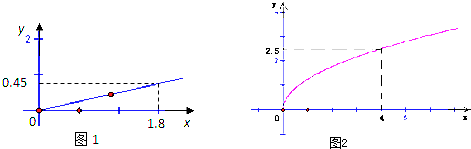
��1���ֱ�A��B���ֲ�Ʒ�������ʾΪͶ�ʵĺ�����ϵʽ��
��2���ü�ͥ����10��Ԫ�ʽ𣬲�ȫ��Ͷ��ծȯ���ȼ��Ͳ�ƷA����Ʊ�ȷ����Ͳ�ƷB���ֲ�Ʒ���ʣ�����������10��ԪͶ�ʣ�����ʹͶ�ʻ��������棬���������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������![]() �ĵ��������Σ���
�ĵ��������Σ���![]() ,
, ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
��![]() �е㣬
�е㣬 ![]() ��
��
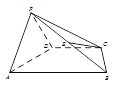
��������֤�� ![]() ƽ��
ƽ��![]() ��
��
��������![]() ��
�� ![]() ����ֱ��
����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵĴ�С��
���ɽǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� ��a1=2��an+1= ![]() Sn��n=1��2��3��������
Sn��n=1��2��3��������
��1��֤��������{ ![]() }�ǵȱ����У�
}�ǵȱ����У�
��2����bn= ![]() ��������{bn}��ǰn���Tn ��
��������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪PΪ��Բ ![]() =1�ϵ�һ���㣬M��N�ֱ�ΪԲ��x+3��2+y2=1��Բ��x��3��2+y2=4�ϵĵ㣬��|PM|+|PN|����СֵΪ ��
=1�ϵ�һ���㣬M��N�ֱ�ΪԲ��x+3��2+y2=1��Բ��x��3��2+y2=4�ϵĵ㣬��|PM|+|PN|����СֵΪ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com