
A、
| ||
B、
| ||
C、
| ||
D、
|
| 区域Ω2的面积 |
| 区域Ω1的面积 |
 解:根据题意可得集合A={(x,y)|x2+y2≤4}所表示的区域即为如图所表示的圆及内部的平面区域,面积为4π,
解:根据题意可得集合A={(x,y)|x2+y2≤4}所表示的区域即为如图所表示的圆及内部的平面区域,面积为4π,| 1 |
| 2 |
| 2 |
| 4π |
| 1 |
| 2π |
| 基本事件所构成区域的长度、面积、体积 |
| 试验的全部结果所构成的区域的长度、面积、体积 |


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源:2012-2013学年云南师大附中高考适应性月考数学试卷3(文科)(解析版) 题型:选择题
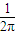



查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省聊城一中高三(下)3月月考数学试卷(理科)(解析版) 题型:选择题
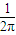


查看答案和解析>>
科目:高中数学 来源:2012年广东省茂名市高考数学一模试卷(文科)(解析版) 题型:选择题
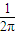


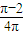
查看答案和解析>>
科目:高中数学 来源:2011年北京市丰台区高考数学一模试卷(文科)(解析版) 题型:选择题
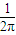


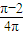
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com