
分析 (Ⅰ)将x=1代入$\frac{x^2}{4}+\frac{y^2}{2}=1$,求得$|AB|\;=\sqrt{6}$,当M为椭圆C的顶点(-2,0)时,M到直线x=1的距离取得最大值3,即可求得△MAB面积的最大值;
(Ⅱ)由题意可知:设M(x0,y0),则有${x_0}^2+2{y_0}^2=4$,则直线MA的方程为$y-n=\frac{{{y_0}-n}}{{{x_0}-t}}(x-t)$,令y=0,得$x=\frac{{t{y_0}-n{x_0}}}{{{y_0}-n}}$,从而$|{OE}|=|{\frac{{t{y_0}-n{x_0}}}{{{y_0}-n}}}|$,同理即可求得$|{OF}|=|{\frac{{t{y_0}+n{x_0}}}{{{y_0}+n}}}|$,则$|{OE}|•|{OF}|=|{\frac{{t{y_0}-n{x_0}}}{{{y_0}-n}}}|•|{\frac{{t{y_0}+n{x_0}}}{{{y_0}+n}}}|$=$|{\frac{{{t^2}y_0^2-{n^2}x_0^2}}{{y_0^2-{n^2}}}}|$=$|{\frac{{4{y_0}^2-4{n^2}}}{{{y_0}^2-{n^2}}}}|$=4.
解答 解:(Ⅰ)当t=1时,将x=1代入$\frac{x^2}{4}+\frac{y^2}{2}=1$,
解得:$y=±\frac{{\sqrt{6}}}{2}$,
∴$|AB|\;=\sqrt{6}$.[(2分)]
当M为椭圆C的顶点(-2,0)时,M到直线x=1的距离取得最大值3,[(4分)]
∴△MAB面积的最大值是$\frac{{3\sqrt{6}}}{2}$.[(5分)]
(Ⅱ)设A,B两点坐标分别为A(t,n),B(t,-n),从而t2+2n2=4.[(6分)]
设M(x0,y0),则有${x_0}^2+2{y_0}^2=4$,x0≠t,y0≠±n.[(7分)]
直线MA的方程为$y-n=\frac{{{y_0}-n}}{{{x_0}-t}}(x-t)$,[(8分)]
令y=0,得$x=\frac{{t{y_0}-n{x_0}}}{{{y_0}-n}}$,从而$|{OE}|=|{\frac{{t{y_0}-n{x_0}}}{{{y_0}-n}}}|$.[(9分)]
直线MB的方程为$y+n=\frac{{{y_0}+n}}{{{x_0}-t}}(x-t)$,[(10分)]
令y=0,得$x=\frac{{t{y_0}+n{x_0}}}{{{y_0}+n}}$,从而$|{OF}|=|{\frac{{t{y_0}+n{x_0}}}{{{y_0}+n}}}|$.[(11分)]
所以$|{OE}|•|{OF}|=|{\frac{{t{y_0}-n{x_0}}}{{{y_0}-n}}}|•|{\frac{{t{y_0}+n{x_0}}}{{{y_0}+n}}}|$=$|{\frac{{{t^2}y_0^2-{n^2}x_0^2}}{{y_0^2-{n^2}}}}|$,
=$|{\frac{{({4-2{n^2}})y_0^2-{n^2}({4-2y_0^2})}}{{y_0^2-{n^2}}}}|$,[(13分)]
=$|{\frac{{4{y_0}^2-4{n^2}}}{{{y_0}^2-{n^2}}}}|$=4.
∴|OE|•|OF|为定值.[(14分)]
点评 本题考查直线与椭圆的位置关系的应用,考查三角形的面积公式,直线的点斜式方程,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<1} | B. | {x|1<x<2} | C. | {x|-1<x<0} | D. | {x|-1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
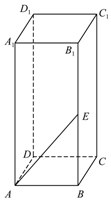 如图所示,长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.过点A1,D1,E的平面α与此长方体的面相交,交线围成一个四边形.
如图所示,长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.过点A1,D1,E的平面α与此长方体的面相交,交线围成一个四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com