
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)是否存在常数![]() ,使得对于定义域内的任意
,使得对于定义域内的任意![]() ,
, ![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】同时抛掷甲、乙两颗骰子.
(1)求事件A“甲的点数大于乙的点数”的概率;
(2)若以抛掷甲、乙两颗骰子点数m,n作为点P的坐标(m,n),求事件B“P落在圆![]() 内”的概率.
内”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四边形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,
轴上,![]() ,且对角线
,且对角线![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() 是直线
是直线![]() 上任意一点,过点
上任意一点,过点![]() 作点
作点![]() 的轨迹
的轨迹![]() 的两切线
的两切线![]() ,
,![]() 为切点,直线
为切点,直线![]() 是否恒过一定点?若是,请求出这个定点的坐标;若不是,请说明理由.
是否恒过一定点?若是,请求出这个定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深![]() (米)是随着一天的时间
(米)是随着一天的时间![]() 呈周期性变化,某天各时刻
呈周期性变化,某天各时刻![]() 的水深数据的近似值如下表:
的水深数据的近似值如下表:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 2.4 | 1.5 | 0.6 | 1.4 | 2.4 | 1.6 | 0.6 | 1.5 |
(Ⅰ)根据表中近似数据画出散点图(坐标系在答题卷中).观察散点图,从
①![]() , ②
, ②![]() ,③
,③![]()
![]() 中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ) 中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全。
中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ) 中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1) 若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围;
(2) 已知函数f(x)=x2+2mx+3m+4.
① 若函数f(x)有且仅有一个零点,求实数m的值;
若函数f(x)有两个零点且两个零点均比-1大,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
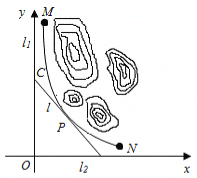
【题目】 某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路的山区边界的直线型公路,记两条相互垂直的公路为![]() ,山区边界曲线为
,山区边界曲线为![]() ,计划修建的公路为
,计划修建的公路为![]() ,如图所示,
,如图所示,![]() 为
为![]() 的两个端点,测得点
的两个端点,测得点![]() 到
到![]() 的距离分别为5千米和40千米,点
的距离分别为5千米和40千米,点![]() 到
到![]() 的距离分别为20千米和2.5千米,以
的距离分别为20千米和2.5千米,以![]() 所在的直线分别为
所在的直线分别为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,假设曲线
,假设曲线![]() 符合函数
符合函数![]() (其中
(其中![]() 为常数)模型.
为常数)模型.
(1)求![]() 的值;
的值;
(2)设公路![]() 与曲线
与曲线![]() 相切于
相切于![]() 点,
点,![]() 的横坐标为
的横坐标为![]() .
.
①请写出公路![]() 长度的函数解析式
长度的函数解析式![]() ,并写出其定义域;
,并写出其定义域;
②当![]() 为何值时,公路
为何值时,公路![]() 的长度最短?求出最短长度.
的长度最短?求出最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 是椭圆
是椭圆![]() 的右焦点,
的右焦点, ![]() 的斜率为
的斜率为![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,当
两点,当![]() 面积最大时,求
面积最大时,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com