
【题目】已知圆![]() ,椭圆
,椭圆![]() (
(![]() )的短轴长等于圆
)的短轴长等于圆![]() 半径的
半径的![]() 倍,
倍,![]() 的离心率为
的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切,证明:
相切,证明:![]() 为直角三角形.
为直角三角形.
【答案】(1)![]() ; (2)证明见解析.
; (2)证明见解析.
【解析】
(1)根据椭圆的几何性质即可求出![]() 的方程;
的方程;
(2)法一,分直线斜率不存在和存在两种情况,求出点坐标利用向量数量积即可证明,法二,分和![]() 轴平行和不平行两种情况,后和法一一样.
轴平行和不平行两种情况,后和法一一样.
(1)因为圆![]() 的半径为
的半径为![]() ,
,
所以![]() 的短轴长为
的短轴长为![]() ,
,
所以![]() ,解得
,解得![]() .
.
因为![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ①,
①,
又因为![]() ,所以
,所以![]() ②,
②,
联立①② ,解得![]() ,
,
所以所求![]() 的方程为
的方程为![]()
(2)证明:证法一:①当直线![]() 斜率不存在时, 直线
斜率不存在时, 直线![]() 的方程为
的方程为![]() .
.
当![]() 时,
时,![]()
所以![]()
当![]() 时,
时,![]()
所以![]() ,
,
综上,![]()
所以![]() 为直角三角形.
为直角三角形.
②当直线![]() 斜率存在时,设其方程为
斜率存在时,设其方程为![]()
![]() 直线
直线![]() 与圆相切,
与圆相切,![]()
即![]() ,
,
由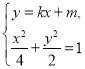 得,
得,![]() ,
,
所以![]()
所以![]()
![]()
![]()
![]()
![]()
所以![]()
综上所述:![]() 所以
所以![]() 为直角三角形.
为直角三角形.
证法二:①当直线方程为![]() 时,
时,
![]()
所以![]() 所以
所以![]() 为直角三角形.
为直角三角形.
②当直线方程为![]() 时,
时,![]()
所以![]() 所以
所以![]() 为直角三角形.
为直角三角形.
③当直线![]() 不与
不与![]() 轴平行时,设其方程为
轴平行时,设其方程为![]()
因为直线![]() 与圆相切,所以
与圆相切,所以![]() ,即
,即![]()
由 得,
得,![]()
所以![]()
![]()
![]()
![]()
![]()
![]()
所以![]() 所以
所以![]() 为直角三角形.
为直角三角形.
综上所述: ![]() 为直角三角形.
为直角三角形.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】新中国成立70周年,社会各界以多种形式的庆祝活动祝福祖国,其中,“快闪”因其独特新颖的传播方式吸引大众眼球.根据腾讯指数大数据,关注“快闪”系列活动的网民群体年龄比例构成,及男女比例构成如图所示,则下面相关结论中不正确的是( )
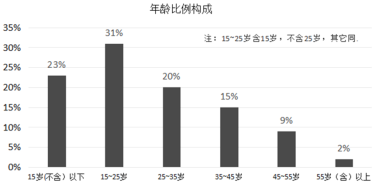
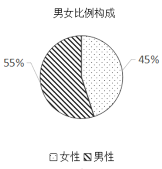
A.35岁以下网民群体超过70%
B.男性网民人数多于女性网民人数
C.该网民群体年龄的中位数在15~25之间
D.25~35岁网民中的女性人数一定比35~45岁网民中的男性人数多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为双曲线
为双曲线![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴的上方交双曲线C于点M,且
轴的上方交双曲线C于点M,且![]()
(1)求双曲线C的方程;
(2)过双曲线C上任意一点P作该双曲线两条渐近线的垂线,垂足分别为![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若![]() 是定义在
是定义在![]() 上的单调函数,求实数a的取值范围;
上的单调函数,求实数a的取值范围;
(2)当![]() 时,判断
时,判断![]() 与
与![]() 的图象在其公共点处是否存在公切线?若存在,求满足条件的a值的个数;若不存在,请说明理由.
的图象在其公共点处是否存在公切线?若存在,求满足条件的a值的个数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
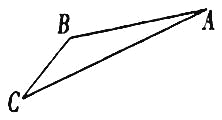
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题
①命题“若![]() ,则
,则![]() ”的逆命题是真命题;
”的逆命题是真命题;
②若![]() ,
,![]() ,则
,则![]() 在
在![]() 上的投影是
上的投影是![]() ;
;
③在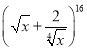 的二项展开式中,有理项共有4项;
的二项展开式中,有理项共有4项;
④已知一组正数![]() ,
,![]() ,
,![]() ,
,![]() 的方差为
的方差为![]() ,则数据
,则数据![]() ,
,![]() ,
,![]() ,
,![]() 的平均数为4;
的平均数为4;
⑤复数![]() 的共轭复数是
的共轭复数是![]() ,则
,则![]() .
.
其中真命题的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ;
;
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若![]() ,且
,且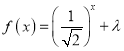 在闭区间
在闭区间![]() 上有实数解,求实数
上有实数解,求实数![]() 的范围;
的范围;
(3)如果函数![]() 的图象过点
的图象过点![]() ,且不等式
,且不等式![]() 对任意
对任意![]() 均成立,求实数
均成立,求实数![]() 的取值集合.
的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com