
【题目】(2015·湖北)已知数列![]() 的各项均为正数,
的各项均为正数,![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(1)求函数![]() 的单调区间,并比较
的单调区间,并比较![]() 与
与![]() 的大小;
的大小;
(2)计算![]() ,
, ![]() ,
, ![]() , 由此推测计算
, 由此推测计算![]() 的公式,并给出证明;
的公式,并给出证明;
(3)令![]() , 数列
, 数列![]() ,
, ![]() 的前
的前![]() 项和分别记为
项和分别记为![]() ,
,![]() , 证明:
, 证明:![]() .
.
【答案】
(1)
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
![]() .
.
(2)
![]() ,
,
下面用数学归纳法证明②。
(1)当![]() 时,左边=右边=2,②成立。
时,左边=右边=2,②成立。
(2)假设当![]() 时,②成立,即
时,②成立,即![]() .当
.当![]() 时,
时,![]() ,有归纳假设可得
,有归纳假设可得![]()
![]() .所以当
.所以当![]() 时,②也成立。根据(1)(2),可知②对一切正整数
时,②也成立。根据(1)(2),可知②对一切正整数![]() 都成立。
都成立。
(3)
【解析】1.![]() 的定义域为
的定义域为![]() ,
, ![]() .当
.当![]() , 即
, 即![]() 时,
时,![]() 单调递增;当
单调递增;当![]() , 即
, 即![]() 时,
时,![]() 单调递减。故
单调递减。故![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .当
.当![]() 时,
时,![]() ,即
,即![]() .令
.令![]() ,得
,得![]() ,即
,即![]() .①
.①
2.![]() ;
;![]() ;
;![]() .由此推测:
.由此推测:![]() ,②
,②
下面用数学归纳法证明②。
(1)当![]() 时,左边=右边=2,②成立。
时,左边=右边=2,②成立。
(2)假设当![]() 时,②成立,即
时,②成立,即![]() .当
.当![]() 时,
时,![]() ,有归纳假设可得
,有归纳假设可得![]()
![]() .所以当
.所以当![]() 时,②也成立。根据(1)(2),可知②对一切正整数
时,②也成立。根据(1)(2),可知②对一切正整数![]() 都成立。
都成立。
3.
由![]() 的定义,② , 算术-集合平均不等式,
的定义,② , 算术-集合平均不等式,![]() 的定义及①得
的定义及①得![]()
![]()
![]()
![]()
![]()
![]()
![]() .即
.即![]() .
.
【考点精析】本题主要考查了基本不等式和数列的定义和表示的相关知识点,需要掌握基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() ;数列中的每个数都叫这个数列的项.记作an,在数列第一个位置的项叫第1项(或首项),在第二个位置的叫第2项,……,序号为n的项叫第n项(也叫通项)记作an才能正确解答此题.
;数列中的每个数都叫这个数列的项.记作an,在数列第一个位置的项叫第1项(或首项),在第二个位置的叫第2项,……,序号为n的项叫第n项(也叫通项)记作an才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】(2015·四川)一辆小客车上有5个座位,其座位号为1,2,3,4,5,乘客P1 , P2 , P3 , P4 , P5的座位号分别为1,2,3,4,5,他们按照座位号顺序先后上车,乘客P1因身体原因没有坐自己号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位.如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
(1)(I)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
乘客 | P1 | P2 | P3 | P4 | P5 |
座位号 | 3 | 2 | 1 | 4 | 5 |
3 | 2 | 4 | 5 | 1 | |
(2)(Ⅱ)若乘客P1坐到了2号座位,其他乘客按规则就坐,求乘客P1坐到5号座位的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点。
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线AC1与平面AA1BB1所成的角为45°,求三棱锥F-AEC的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马P-ABCD中,侧棱![]() 底面
底面![]() ,且
,且![]() ,过棱
,过棱![]() 的中点
的中点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]()
(1)证明:![]() 平面
平面![]() .试判断四面体
.试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写
是否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,说明理由;
(2)若面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() , 求
, 求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015![]() 福建)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
福建)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.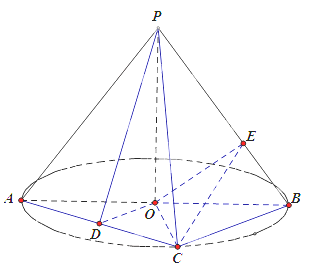
(1)若D为线段AC的中点,求证AC![]() 平面PDO;
平面PDO;
(2)求三棱锥P-ABC体积的最大值;
(3)若BC=![]() ,点E在线段PB上,求CE+OE的最小值.
,点E在线段PB上,求CE+OE的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()
(Ⅰ)求频率分布图中a的值;
(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;
(Ⅲ)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率。
的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加. 现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(1)设![]() 为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件
为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件![]() 发生的概率
发生的概率
(2)设![]() 为选出的4人中种子选手的人数,求随机变量
为选出的4人中种子选手的人数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 的对边分别为
的对边分别为![]() 且
且![]() 为锐角,问:(1)证明: B - A =
为锐角,问:(1)证明: B - A = ![]() ,(2)求 sin A + sin C 的取值范围
,(2)求 sin A + sin C 的取值范围
(1)(1)证明:![]()
(2)(2)求![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com