练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    (1)已知a+b=lg32+lg35+3lg2·lg5,求3ab+a3+b3的值；

    (2)设f(x)=logax(a＞0,且a≠1),若f(3)－f(2)=1,求f(3.75)+f(0.9)的值；

    (3)已知方程lg2x+(lg2+lg3)lgx+lg2·lg3=0的两个根为x1、x2,求x1x2的值.

    解:(1)∵lg2+lg5=1,

    ∴a+b=lg32+lg35+3lg2lg5(lg2+lg5)=(lg2+lg5)3=1.

    ∴a3+b3+3ab=a3+b3+3ab·1=a3+b3+3ab(a+b)=(a+b)3=1.

    (2)∵loga3－loga2=1,∴loga=1.∴a=.

    ∴f(3.75)+f(0.9)=loga3.75+loga0.9

    =loga3.375=log()3=3.

    (3)∵lgx1+lgx2=－(lg2+lg3),

    ∴lg(x1x2)=lg.∴x1x2=.

    点评:对数运算性质可以正用，也可以反用.关键是如何用好的问题.只有通过练习，才能掌握运用技巧.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设二次函数 y=f（x）=ax2+bx+c的图象以y轴为对称轴，已知a+b=1，而且若点（x，y）在 y=f（x）的图象上，则点（x，y2+1）在函数 g（x）=f[f（x）]的图象上．
    （1）求g（x）的解析式；
    （2）设F（x）=g（x）-λf（x），问是否存在这样的l（λ∈R），使f（x）在(-∞，-
    		2
    2
    )    内是减函数，在（-
    		2
    2
    ，0）内是增函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：022

    已知点A，B，直线l及平面a，b，用符号：“Î，Ï，Ì，Ë”填空：

        （1）已知AÎa，aÌb，则A________b；

        （2）已知a∩b=l，A________a，A________b则AÎl；

        （3）已知AÎa，BÎa，AÎb，BÎb，则a________b=________．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：022

    已知点A，B，直线l及平面a，b，用符号：“Î，Ï，Ì，Ë”填空：

        （1）已知AÎa，aÌb，则A________b；

        （2）已知a∩b=l，A________a，A________b则AÎl；

        （3）已知AÎa，BÎa，AÎb，BÎb，则a________b=________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    根据叙述作图，指出二面角a -l-b 的平面角，并证明．

    　　（1）已知a ∩b =l，A∈l（图9-39）．在a 内作PA⊥l于A，在b 内作QA⊥l于A．

    图9-39

    　　（2）已知a ∩b =l，A∈a ，（图9-40）．作AP⊥b 于P，在a 内作AQ⊥l于Q，连结PQ．

    图9-40

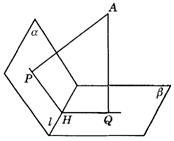
    　　（3）已知a ∩b =l，， （图9-41）．作AP⊥a 于P，AQ⊥b 于Q，l∩平面PAQ=H，连结PH、QH．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年北京师大附中高一（上）期中数学试卷（解析版） 题型：解答题

    设二次函数 y=f（x）=ax2+bx+c的图象以y轴为对称轴，已知a+b=1，而且若点（x，y）在 y=f（x）的图象上，则点（x，y2+1）在函数 g（x）=f[f（x）]的图象上．
    （1）求g（x）的解析式；
    （2）设F（x）=g（x）-λf（x），问是否存在这样的l（λ∈R），使f（x）在内是减函数，在（，0）内是增函数．

    查看答案和解析>>

    同步练习册答案