
分析 由诱导公式可得sin($\frac{π}{4}$+x)=cos($\frac{π}{4}$-x),整体代入要求的式子结合三角函数公式化简可得.
解答 解:由诱导公式可得sin($\frac{π}{4}$+x)=sin[$\frac{π}{2}$-($\frac{π}{4}$-x)]=cos($\frac{π}{4}$-x),
∴$\frac{2co{s}^{4}x-2co{s}^{2}x+\frac{1}{2}}{2tan(\frac{π}{4}-x)si{n}^{2}(\frac{π}{4}+x)}$=$\frac{\frac{1}{2}(4co{s}^{4}x-4co{s}^{2}x+1)}{2•\frac{sin(\frac{π}{4}-x)}{cos(\frac{π}{4}-x)}•co{s}^{2}(\frac{π}{4}-x)}$
=$\frac{\frac{1}{2}(2co{s}^{2}x-1)^{2}}{2sin(\frac{π}{4}-x)cos(\frac{π}{4}-x)}$=$\frac{\frac{1}{2}(cos2x)^{2}}{sin(\frac{π}{2}-2x)}$=$\frac{\frac{1}{2}(cos2x)^{2}}{cos2x}$=$\frac{1}{2}$cos2x.
点评 本题考查三角函数的化简求值,涉及诱导公式和二倍角公式以及整体思想,属中档题.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{5}{3}$,$\frac{5}{2}$] | B. | (-∞,-$\frac{5}{3}$]∪[$\frac{5}{2}$,+∞) | C. | (-∞,-$\frac{5}{2}$]∪[$\frac{5}{3}$,+∞) | D. | [-$\frac{5}{2}$,$\frac{5}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,+∞) | B. | (-∞,0) | C. | (0,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
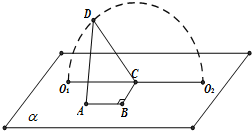 如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 计算1+2+…+n | B. | 计算1+(1+2)+(1+2+3)+…(1+2+3+…+n) | ||
| C. | 计算n! | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com