
【题目】下列函数中,是偶函数且在区间(0,+∞)上单调递减的函数是( )
A.y=2x
B.y= ![]()
C.y=2 ![]()
D.y=﹣x2
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( ) 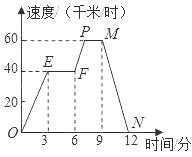
A.第3分时汽车的速度是40千米/时
B.第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车行驶了120千米
D.从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,圆
轴的正半轴重合,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为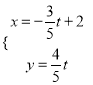 (
(![]() 为参数).
为参数).
(Ⅰ)若![]() ,
, ![]() 是直线
是直线![]() 与
与![]() 轴的交点,
轴的交点, ![]() 是圆
是圆![]() 上一动点,求
上一动点,求![]() 的最大值;
的最大值;
(Ⅱ)若直线![]() 被圆
被圆![]() 截得的弦长等于圆
截得的弦长等于圆![]() 的半径
的半径![]() 倍,求
倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=x2|x﹣a|(a∈R).21世纪教育网
(1)判定f(x)的奇偶性,并说明理由;
(2)当a≠0时,是否存在一点M(t,0),使f(x)的图象关于点M对称,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集为实数集R,集合A={x|y= ![]() +
+ ![]() },B={x|log2x>1}.
},B={x|log2x>1}.
(1)分别求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
设函数![]()
(Ⅰ)若![]() 是函数
是函数![]() 的极值点,1和
的极值点,1和![]() 是
是![]() 的两个不同零点,且
的两个不同零点,且![]()
且![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若对任意![]() , 都存在
, 都存在![]() (
(![]() 为自然对数的底数),使得
为自然对数的底数),使得![]()
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com