
【题目】已知四边形ABCD满足AD∥BC,BA=AD=DC= ![]() BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F,G分别为B1D,AE的中点.
BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F,G分别为B1D,AE的中点. 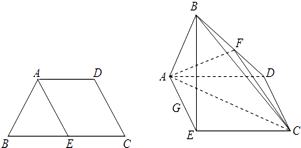
(1)求三棱锥E﹣ACB1的体积;
(2)证明:B1E∥平面ACF;
(3)证明:平面B1GD⊥平面B1DC.
【答案】
(1)解:由题意知,AD∥EC且AD=EC,所以四边形ADCE为平行四边形,
∴AE=DC=a,
∴△ABE为等边三角形,
∴∠AEC=120°,
∴ ![]()
连结B1G,则B1G⊥AE,又平面B1AE⊥平面AECD交线AE,
∴B1G⊥平面AECD且 ![]()
∴ ![]()
(2)证明:连接ED交AC于O,连接OF,
∵AEDC为菱形,且F为B1D的中点,
∴FO∥B1E,
又B1E面ACF,FO平面ACF,
∴B1E∥平面ACF
(3)证明:连结GD,则DG⊥AE,又B1G⊥AE,B1G∩GD=G,
∴AE⊥平面B1GD.
又AE∥DC,∴DC⊥平面B1GD,又DC平面B1DC
∴平面B1GD⊥平面B1DC.

【解析】(1)由题意知,AD∥EC且AD=EC,所以四边形ADCE为平行四边形,得到AE=DC,得到∠AEC=120°,首先求出△AEC的面积,进一步求出高B1G,利用体积公式可求;(2)连接ED交AC于O,连接OF,利用AEDC为菱形,且F为B1D的中点得到FO∥B1E,利用线面平行的判定定理可证;(3)证明:连结GD,则DG⊥AE,又B1G⊥AE,B1G∩GD=G,判断AE⊥平面B1GD,利用面面垂直的判定定理可证.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案科目:高中数学 来源: 题型:
【题目】![]() 是直线
是直线![]() 与函数
与函数![]() 图像的两个相邻的交点,且
图像的两个相邻的交点,且![]() .
.
(1)求![]() 的值和函数
的值和函数![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象上各点的横坐标伸长为原来的
的图象上各点的横坐标伸长为原来的![]() 倍(纵坐标不变),再将得到的图象向左平移
倍(纵坐标不变),再将得到的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 的对称轴方程.
的对称轴方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足条件(n﹣1)an+1=(n+1)(an﹣1),且a2=6,
(1)计算a1、a3、a4 , 请猜测数列{an}的通项公式并用数学归纳法证明;
(2)设bn=an+n(n∈N*),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个四棱锥的三视图如图所示,关于这个四棱锥,下列说法正确的是( )

A. 最长的棱长为![]()
B. 该四棱锥的体积为![]()
C. 侧面四个三角形都是直角三角形
D. 侧面三角形中有且仅有一个等腰三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为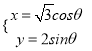 (
(![]() 为参数).以平面直角坐标系
为参数).以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,取相同的单位长度建立极坐标系,直线
轴正半轴为极轴,取相同的单位长度建立极坐标系,直线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点. 
(1)证明B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的正弦值.
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ![]() ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲乙两班各6名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图,则甲班样本数据的众数和乙班样本数据的中位数分别是( ) 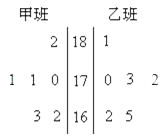
A.170,170
B.171,171
C.171,170
D.170,172
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:“ ![]() =1是焦点在x轴上的椭圆的标准方程”,命题q:“不等式组
=1是焦点在x轴上的椭圆的标准方程”,命题q:“不等式组  所表示的区域是三角形”.若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
所表示的区域是三角形”.若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com