
【题目】已知![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时, 证明
时, 证明![]() 对于任意的
对于任意的![]() 成立.
成立.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减, 当
内单调递减, 当![]() 时,
时,![]() 在
在![]() 内单调递增,在
内单调递增,在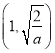 内单调递减,在
内单调递减,在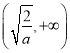 内单调递增,当
内单调递增,当![]() 时,
时,![]() 在
在![]() 内单调递增, 当
内单调递增, 当![]() 时,
时,![]() 在
在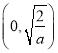 内单调递增,在
内单调递增,在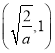 内单调递减, 在
内单调递减, 在![]() 单调递增;(2)证明见解析.
单调递增;(2)证明见解析.
【解析】
试题分析:(1)求出原函数的导函数,然后对![]() 分类分析导函数的符号,由导函数的符号确定原函数的单调性;
分类分析导函数的符号,由导函数的符号确定原函数的单调性;
(2)构造函数![]() ,令
,令![]() ,
,![]() .则
.则
![]() ,利用导数分别求
,利用导数分别求![]() 与
与![]() 的最小值得到
的最小值得到![]() 恒成立.由此可得
恒成立.由此可得![]() 对于任意的
对于任意的![]() 成立.
成立.
试题解析:(1)![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时,![]() 时,
时,![]() 单调递增,
单调递增, ![]() 时,
时, ![]() 单调递减, 当
单调递减, 当![]() 时,
时,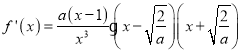 .
.
①![]() 时,
时,![]() , 当
, 当![]() 或
或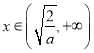 时,
时,![]() 单调递增, 当
单调递增, 当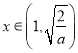 时,
时, ![]() 单调递减.
单调递减.
②![]() 时,
时,![]() , 在
, 在![]() 内,
内, ![]() 单调递增.
单调递增.
③当![]() 时,
时,![]() , 当
, 当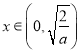 或
或![]() 时,
时, ![]() 单调递增, 当
单调递增, 当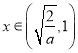 时,
时, ![]() 单调递减.
单调递减.
综上所述, 当![]() 时,
时,![]() 在
在![]() 内单调递增, 在
内单调递增, 在![]() 内单调递减, 当
内单调递减, 当![]() 时,
时, ![]() 在
在![]() 内单调递增, 在
内单调递增, 在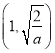 内单调递减, 在
内单调递减, 在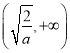 内单调递增, 当
内单调递增, 当![]() 时,
时,![]() 在
在![]() 内单调递增, 当
内单调递增, 当![]() 时,
时, ![]() 在
在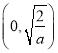 内单调递增, 在
内单调递增, 在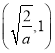 内单调递减, 在
内单调递减, 在![]() 单调递增.
单调递增.
(2)证明: 由(1)知![]() 时,
时,
![]() ,
,
设![]() ,则
,则![]() ,
,
由![]() ,可得
,可得![]() ,当且仅当
,当且仅当![]() 时取得等号, 又
时取得等号, 又![]() ,
,
设![]() ,则
,则![]() 在
在![]() 单调递减, 因为
单调递减, 因为![]() ,
,
使得![]() 时,
时,![]() 时,
时,![]() 在
在![]() 内单调递增, 在
内单调递增, 在![]() 内单调递减, 由
内单调递减, 由![]() ,可得
,可得![]() ,当且仅当
,当且仅当![]() 时取得等号, 所以
时取得等号, 所以![]() ,即
,即![]() 对于任意的
对于任意的![]() 成立.
成立.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】从一箱产品中随机地抽取一件,设事件A=“抽到一等品”,事件B = “抽到二等品”,事件C =“抽到三等品”,且已知 P(A)= 0.65 ,P(B)=0.2 ,P(C)=0.1。则事件“抽到的不是一等品”的概率为( )
A. 0.65 B. 0.35 C. 0.3 D. 0.005
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对某校1 200名学生的耐力进行调查,抽取其中120名学生,测试他们1 500 m跑步的成绩,得出相应的数值,在这项调查中,样本是指( )
A. 120名学生 B. 1 200名学生
C. 120名学生的成绩 D. 1 200名学生的成绩
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列几个命题:①三点确定一个平面;②一个点和一条直线确定一个平面;③垂直于同一直线的两直线平行;④平行于同一直线的两直线平行.其中正确命题的序号是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛,经过初赛,复赛,甲、乙两个代表队,(每队![]() 人)进入了决赛,规定每人回答一个问题,答对为本队赢得
人)进入了决赛,规定每人回答一个问题,答对为本队赢得![]() 分,答错得
分,答错得![]() 分,假设甲队中每人答对的概率均为
分,假设甲队中每人答对的概率均为![]() ,乙队中
,乙队中![]() 人答对的概率分别为
人答对的概率分别为![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(1)求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)求甲、乙两队总得分之和等于![]() 分且甲队获胜的概率.
分且甲队获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为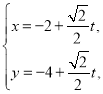 (
(![]() 为参数),
为参数),![]() 与
与![]() 分别交于
分别交于![]() .
.
(Ⅰ)写出![]() 的平面直角坐标系方程和
的平面直角坐标系方程和![]() 的普通方程;
的普通方程;
(Ⅱ)若![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 顺序结构是由若干个依次执行的处理步骤组成的,每一个算法都离不开顺序结构
B. 循环结构是在一些算法中从某处开始按照一定条件,反复执行某一处理步骤,故循环结构中一定包含条件分支结构
C. 循环结构中不一定包含条件分支结构
D. 循环结构中反复执行的处理步骤叫做循环体
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com