
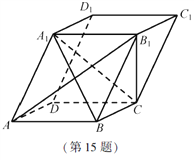
【题目】在平行六面体![]() 中,
中,![]() .
.

求证:(1)![]() ;
;
(2)![]() .
.
【答案】答案见解析
【解析】分析:(1)先根据平行六面体得线线平行,再根据线面平行判定定理得结论;(2)先根据条件得菱形ABB1A1,再根据菱形对角线相互垂直,以及已知垂直条件,利用线面垂直判定定理得线面垂直,最后根据面面垂直判定定理得结论.
详解:
证明:(1)在平行六面体ABCD-A1B1C1D1中,AB∥A1B1.
因为AB![]() 平面A1B1C,A1B1
平面A1B1C,A1B1![]() 平面A1B1C,
平面A1B1C,
所以AB∥平面A1B1C.
(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形.
又因为AA1=AB,所以四边形ABB1A1为菱形,
因此AB1⊥A1B.
又因为AB1⊥B1C1,BC∥B1C1,
所以AB1⊥BC.
又因为A1B∩BC=B,A1B![]() 平面A1BC,BC
平面A1BC,BC![]() 平面A1BC,
平面A1BC,
所以AB1⊥平面A1BC.
因为AB1![]() 平面ABB1A1,
平面ABB1A1,
所以平面ABB1A1⊥平面A1BC.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)求f(2)+f![]() ,f(3)+f
,f(3)+f![]() 的值;
的值;
(2)求证:f(x)+f![]() 是定值;
是定值;
(3)求f(2)+f![]() +f(3)+f
+f(3)+f![]() +…+
+…+![]() +f
+f![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣1:几何证明选讲
如图,⊙O和⊙O′相交于A,B两点,过A作两圆的切线分别交两圆于C、D两点,连接DB并延长交⊙O于点E.证明:
(1)ACBD=ADAB;
(2)AC=AE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在空间四边形ABCD中,点E,H分别是边AB,AD的中点,点F,G分别是边BC,CD上的点,且![]() ,则下列说法正确的是________.(填写所有正确说法的序号)
,则下列说法正确的是________.(填写所有正确说法的序号)

①EF与GH平行; ②EF与GH异面;
③EF与GH的交点M可能在直线AC上,也可能不在直线AC上;
④EF与GH的交点M一定在直线AC上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三梭柱ABC﹣A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
(1)求证:E是AB中点;
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() :
: ![]() (
(![]() )上一点,
)上一点, ![]() 是抛物线的焦点,
是抛物线的焦点, ![]() 且
且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知![]() ,过
,过![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,以
两点,以![]() 为圆心的圆
为圆心的圆![]() 与直线
与直线![]() 相切,试判断圆
相切,试判断圆![]() 与直线
与直线![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com