
| A. | $\frac{1}{6}$ | B. | $\frac{5}{36}$ | C. | $\frac{7}{36}$ | D. | $\frac{5}{12}$ |
分析 本题是一个等可能事件的概率,试验发生包含的事件是6×6种结果,满足条件的事件需要先整理出关于x,y之间的关系,得到2x<y,根据条件列举出可能的情况,根据概率公式得到结果.
解答 解:由题意知,本题是一个等可能事件的概率,
试验发生包含的事件是6×6=36种结果,
∵log2xy>1,
∴2x<y,
∵x∈{1,2,3,4,5,6},y∈{1,2,3,4,5,6},
∴共有:(1,3),(1,4),(1,5),(2,5),(1,6),(2,6),共6种情况.
∴P=$\frac{6}{36}$=$\frac{1}{6}$,
故选:A
点评 本题考查等可能事件的概率,考查对数的运算,通过列举的方法得到需要的结果,本题是一个综合题,注意对于对数式的整理.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y-2)2=1 | B. | x2+(y-1)2=1 | C. | (x+1)2+(y-1)2=1 | D. | (x+2)2+(y-1)2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
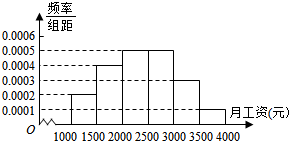 进入2014年金秋,新入职的大学生陆续拿到了第一份薪水.某地调查机构就月薪情况调查了1000名新入职大学生,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月薪在[1000,1500)单位:元).
进入2014年金秋,新入职的大学生陆续拿到了第一份薪水.某地调查机构就月薪情况调查了1000名新入职大学生,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月薪在[1000,1500)单位:元).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π-α | B. | α | C. | $\frac{π}{2}$-α | D. | $\frac{3π}{2}$-α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 菱形 | C. | 等腰梯形 | D. | 不等腰梯形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
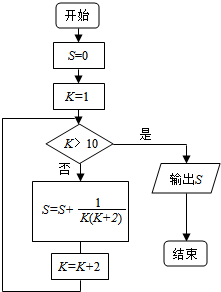
| A. | $\frac{5}{11}$ | B. | $\frac{5}{13}$ | C. | $\frac{4}{9}$ | D. | $\frac{6}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com