
(07年湖南卷理)(12分)
如图2,![]() 分别是矩形
分别是矩形![]() 的边
的边![]() 的中点,
的中点,![]() 是
是![]() 上的一点,将
上的一点,将![]() ,
,![]() 分别沿
分别沿![]() 翻折成
翻折成![]() ,
,![]() ,并连结
,并连结![]() ,使得平面
,使得平面![]()
平面![]() ,
,![]() ,且
,且![]() .连结
.连结![]() ,如图3.
,如图3.
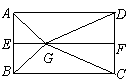
图2

图3
(I)证明:平面![]() 平面
平面![]() ;
;
(II)当![]() ,
,![]() ,
,![]() 时,求直线
时,求直线![]() 和平面
和平面![]() 所成的角.
所成的角.
解析:解法一:(I)因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]()
![]() 平面
平面![]() .
.
(II)过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() .
.
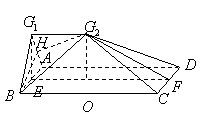
由(I)的结论可知,![]() 平面
平面![]() ,
,
所以![]() 是
是![]() 和平面
和平面![]() 所成的角.
所成的角.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() .
.
因为![]() ,
,![]() ,所以可在
,所以可在![]() 上取一点
上取一点![]() ,使
,使![]() ,
,
又因为![]() ,所以四边形
,所以四边形![]() 是矩形.
是矩形.
由题设![]() ,
,![]() ,
,![]() ,则
,则![]() .所以
.所以![]() ,
,
![]() ,
,![]() ,
,![]() .
.
因为![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,从而
,从而![]() .
.
故![]() ,
,![]() .
.
又![]() ,由
,由![]() 得
得![]() .
.
故![]() .
.
即直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .
.
解法二:(I)因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,从而
,从而![]() .又
.又![]() ,
,
所以![]() 平面
平面![]() .因为
.因为![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() .
.
(II)由(I)可知,![]() 平面
平面![]() .故可以
.故可以![]() 为原点,分别以直线
为原点,分别以直线![]()
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系(如图),
轴建立空间直角坐标系(如图),
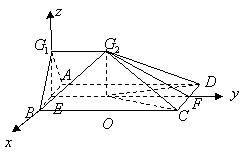
由题设![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,![]() ,相关各点的坐标分别是
,相关各点的坐标分别是![]() ,
,
![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
由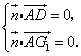 得
得![]() 故可取
故可取![]() .
.
过点![]() 作
作![]() 平面
平面![]() 于点
于点![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
于是点![]() 在
在![]() 轴上.
轴上.
因为![]() ,所以
,所以![]() ,
,![]() .
.
设![]() (
(![]() ),由
),由![]() ,解得
,解得![]() ,
,
所以![]() .
.
设![]() 和平面
和平面![]() 所成的角是
所成的角是![]() ,则
,则
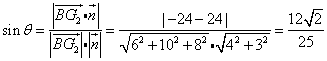 .
.
故直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .
.


科目:高中数学 来源: 题型:
(07年湖南卷理)将杨辉三角中的奇数换成1,偶数换成0,得到如图1所示的0-1三角数表.从上
往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第![]() 次全行的数都为1的是第 行;第61行中1的个数是 .
次全行的数都为1的是第 行;第61行中1的个数是 .
第1行 1 1
第2行 1 0 1
第3行 1 1 1 1
第4行 1 0 0 0 1
第5行 1 1 0 0 1 1
…… ………………………………
图1
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年湖南卷理)(12分)
如图2,![]() 分别是矩形
分别是矩形![]() 的边
的边![]() 的中点,
的中点,![]() 是
是![]() 上的一点,将
上的一点,将![]() ,
,![]() 分别沿
分别沿![]() 翻折成
翻折成![]() ,
,![]() ,并连结
,并连结![]() ,使得平面
,使得平面![]()
平面![]() ,
,![]() ,且
,且![]() .连结
.连结![]() ,如图3.
,如图3.
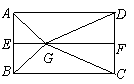
图2
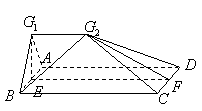
图3
(I)证明:平面![]() 平面
平面![]() ;
;
(II)当![]() ,
,![]() ,
,![]() 时,求直线
时,求直线![]() 和平面
和平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年湖南卷理)(12分)
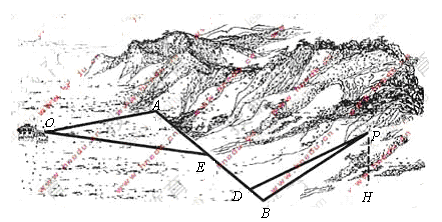
如图4,某地为了开发旅游资源,欲修建一条连接风景点![]() 和居民区
和居民区![]() 的公路,点
的公路,点![]() 所在的山坡面与山脚所在水平面
所在的山坡面与山脚所在水平面![]() 所成的二面角为
所成的二面角为![]() (
(![]() ),且
),且![]() ,点
,点![]() 到平面
到平面![]() 的距离
的距离![]() (km).沿山脚原有一段笔直的公路
(km).沿山脚原有一段笔直的公路![]() 可供利用.从点
可供利用.从点![]() 到山脚修路的造价为
到山脚修路的造价为![]() 万元/km,原有公路改建费用为
万元/km,原有公路改建费用为![]() 万元/km.当山坡上公路长度为
万元/km.当山坡上公路长度为![]() km(
km(![]() )时,其造价为
)时,其造价为![]() 万元.已知
万元.已知![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)在![]() 上求一点
上求一点![]() ,使沿折线
,使沿折线![]() 修建公路的总造价最小;
修建公路的总造价最小;
(II) 对于(I)中得到的点![]() ,在
,在![]() 上求一点
上求一点![]() ,使沿折线
,使沿折线![]()
修建公路的总造价最小.
(III)在![]() 上是否存在两个不同的点
上是否存在两个不同的点![]() ,
,![]() ,使沿折线
,使沿折线![]() 修建公路的
修建公路的
总造价小于(II)中得到的最小总造价,证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com