
【题目】已知函数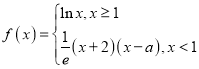 (
(![]() 为常数,
为常数,![]() 为自然对数的底数)的图象在点
为自然对数的底数)的图象在点![]() 处的切线与该函数的图象恰好有三个公共点,则实数
处的切线与该函数的图象恰好有三个公共点,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]() 或
或![]()
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,....599,600从中抽取60个样本,现提供随机数表的第4行到第6行:
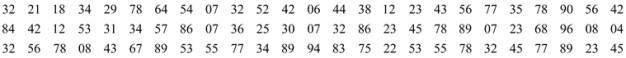
若从表中第6行第6列开始向右依次读取3个数据,则得到的第7个样本编号( )
A.522B.324C.535D.578
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]()
![]() ,如图将
,如图将![]() 分别绕原点
分别绕原点![]() 逆时针旋转
逆时针旋转![]() ,
,![]() ,
,![]() 得到曲线
得到曲线![]() ,
,![]() ,
,![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.

(1)分别写出曲线![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 交
交![]() 于
于![]() 两点,
两点,![]() 交
交![]() 于
于![]() 两点(其中
两点(其中![]() 均不与原点重合),若四边形
均不与原点重合),若四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的台风都对泉州地区的渔业造成较大的经济损失.某保险公司为此开发了针对渔船的险种,并将投保的渔船分为I,II两类,两类渔船的比例如图所示.经统计,2019年I,II两类渔船的台风遭损率分别为![]() 和
和![]() .2020年初,在修复遭损船只的基础上,对I类渔船中的
.2020年初,在修复遭损船只的基础上,对I类渔船中的![]() 进一步改造.保险公司预估这些经过改造的渔船2020年的台风遭损率将降为
进一步改造.保险公司预估这些经过改造的渔船2020年的台风遭损率将降为![]() ,而其他渔船的台风遭损率不变.假设投保的渔船不变,则下列叙述中正确的是( )
,而其他渔船的台风遭损率不变.假设投保的渔船不变,则下列叙述中正确的是( )
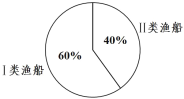
A.2019年投保的渔船的台风遭损率为![]()
B.2019年所有因台风遭损的投保的渔船中,I类渔船所占的比例不超过![]()
C.预估2020年I类渔船的台风遭损率会小于II类渔船的台风遭损率的两倍
D.预估2020年经过进一步改造的渔船因台风遭损的数量少于II类渔船因台风遭损的数量
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科院为试验冬季昼夜温差对反季节大豆新品种发芽的影响,对温差与发芽率之间的关系进行统计分析研究,记录了6天昼夜温差与实验室中种子发芽数的数据如下:
日期 | 1月1日 | 1月2日 | 1月3日 | 1月4日 | 1月5日 | 1月6日 |
温差 | 10 | 11 | 12 | 13 | 8 | 9 |
发芽数 | 26 | 27 | 30 | 32 | 21 | 24 |
他们确定的方案是先从这6组数据中选出2组,用剩下的4组数据求回归方程,再用选取的两组数据进行检验.
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若由线性回归方程得到的估计数据与实际数据的误差不超过1粒,则认为得到的线性回归方程是可靠的.请根据1月2,3,4,5日的数据求出![]() 关于
关于![]() 的线性回归方程(保留两位小数),并检验此方程是否可靠.
的线性回归方程(保留两位小数),并检验此方程是否可靠.
参考公式: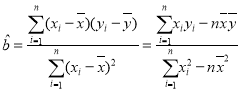 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
(1)若函数![]() 在点
在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,求实数
,求实数![]() 的值;
的值;
(2)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(3)若关于![]() 的不等式
的不等式![]() 在区间
在区间![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是给定的平面,设不在
是给定的平面,设不在![]() 内的任意两点M,N所在的直线为l,则下列命题正确的是( )
内的任意两点M,N所在的直线为l,则下列命题正确的是( )
A.在![]() 内存在直线与直线l异面
内存在直线与直线l异面
B.在![]() 内存在直线与直线l相交
内存在直线与直线l相交
C.在![]() 内存在直线与直线l平行
内存在直线与直线l平行
D.存在过直线l的平面与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AA1=8,AB=3,AD=8,点M是棱AD的中点,点N是棱AA1的中点,P是侧面四边形ADD1A1内一动点(含边界),若C1P∥平面CMN,则线段C1P长度的取值范围是( )
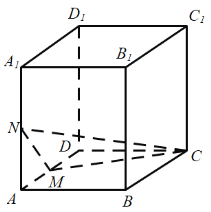
A.![]() B.[4,5]C.[3,5]D.
B.[4,5]C.[3,5]D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com