
| 家电名称 | 空调器 | 彩电 | 冰箱 |
| 工时 |  |  |  |
| 产值(千元) | 4 | 3 | 2 |
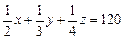 ②
②

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
.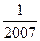 )+f(-
)+f(-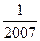 )的值;
)的值; 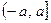 (其中a∈(0, 1), 且a为常数)时,
(其中a∈(0, 1), 且a为常数)时, 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
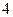 月份,有一新款服装投入某商场销售,
月份,有一新款服装投入某商场销售,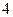 月
月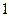 日该款服装仅销售出
日该款服装仅销售出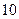 件,第二天售出
件,第二天售出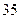 件,第三天销售
件,第三天销售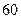 件,然后,每天售出的件数分别递增
件,然后,每天售出的件数分别递增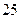 件,直到日销售量达到最大后,每天销售的件数分别递减
件,直到日销售量达到最大后,每天销售的件数分别递减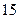 件,到月底该服装共销售出
件,到月底该服装共销售出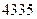 件.(Ⅰ)问
件.(Ⅰ)问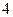 月几号该款服装销售件数最多?其最大值是多少?(Ⅱ)按规律,当该商场销售此服装超过
月几号该款服装销售件数最多?其最大值是多少?(Ⅱ)按规律,当该商场销售此服装超过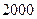 件时,社会上就流行,而日销售量连续下降,并低于
件时,社会上就流行,而日销售量连续下降,并低于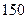 件时,则流行消失,问该款服装在社会上流行是否超过
件时,则流行消失,问该款服装在社会上流行是否超过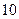 天?并说明理由。
天?并说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
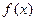 是定义域为[-3,3]的函数,并且设
是定义域为[-3,3]的函数,并且设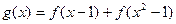 ,
,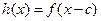 ,其中常数c为实数.(1)求
,其中常数c为实数.(1)求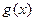 和
和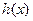 的定义域;(2)如果
的定义域;(2)如果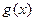 和
和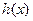 两个函数的定义域的交集为非空集合,求c的取值范围;(3)当
两个函数的定义域的交集为非空集合,求c的取值范围;(3)当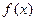 在其定义域内是奇函数,又是增函数时,求使
在其定义域内是奇函数,又是增函数时,求使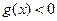 的自变量
的自变量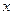 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com