
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据向量加法的几何意义,数量积的定义,共线向量的定义,以及向量数乘的几何意义即可判断每个命题的正误,从而找出正确选项.
解答 解:①$\overrightarrow{AB}=-\overrightarrow{BA}$;
∴$\overrightarrow{AB}+\overrightarrow{BA}=-\overrightarrow{BA}+\overrightarrow{BA}=\overrightarrow{0}$;
∴该命题正确;
②数量积是一个实数,不是向量;
∴该命题错误;
③$\overrightarrow{a}$与$\overrightarrow{b}$共线,且方向相反时,$\overrightarrow{a}•\overrightarrow{b}=-|\overrightarrow{a}||\overrightarrow{b}|$;
∴该命题错误;
④$\overrightarrow{c}$与$\overrightarrow{a}$不共线,且$\overrightarrow{a}•\overrightarrow{b}≠0,\overrightarrow{b}•\overrightarrow{c}≠0$时,$(\overrightarrow{a}•\overrightarrow{b})•\overrightarrow{c}≠\overrightarrow{a}•(\overrightarrow{b}•\overrightarrow{c})$;
∴该命题错误;
∴正确命题的个数为1.
故选A.
点评 考查向量加法和数乘的几何意义,以及数量积和共线向量的定义.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{1}{12},-\frac{4}{49})$ | B. | $[-\frac{1}{12},0]$ | C. | $(-\frac{4}{49},0]$ | D. | $[-\frac{4}{49},0]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
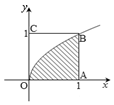 如图,在正方形OABC内任取一点,取到函数$y=\sqrt{x}$的图象与x轴正半轴之间
如图,在正方形OABC内任取一点,取到函数$y=\sqrt{x}$的图象与x轴正半轴之间查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com