已知一圆与直线3x+4y-2=0相切于点P(2,-1),且截x轴的正半轴所得的弦的长为8,求此圆的标准方程.
解:设圆方程为(x-a)
2+(y-b)
2=r
2过P点,且垂直于直线3x+4y-2=0的直线为y+1=

(x-2),即4x-3y-11=0
圆心(a,b)在此直线上,且到点P的距离d=r,即:
①4a-3b-11=0,
②
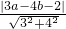
=r
将y=0代入圆方程,得:(x-a)
2+b
2=r
2,
解得x
1=a+
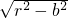
,x
2=a-
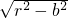
圆截x轴正半轴所得弦长8=|x
1-x
2|=2
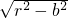
,即r
2-b
2=16 ③
①②③联立解得:r=5,a=5,b=3
所以圆方程为(x-5)
2+(y-3)
2=25
分析:我们可以使用待定系数法求圆的标准方程,即先设圆方程为(x-a)
2+(y-b)
2=r
2,再根据直线3x+4y-2=0相切于点P(2,-1),可得圆心在过P点切与直线3x+4y-2=0垂直的直线上,圆心到直线3x+4y-2=0的距离等于半径,再由截x轴的正半轴所得的弦的长为8,我们可以构造一个关于a,b,r的方程组,解方程组求出a,b,r的值,即可得到此圆的标准方程.
点评:本题考查的知识点是直线与圆相交的性质,圆的标准方程等,求圆的方程一般使用待定系数法,即先设圆方程为(x-a)
2+(y-b)
2=r
2,再根据题目中的其它条件构造一个关于a,b,r的方程组,解方程组求出a,b,r的值,求出圆的方程.

 (x-2),即4x-3y-11=0
(x-2),即4x-3y-11=0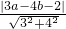 =r
=r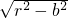 ,x2=a-
,x2=a-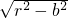
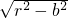 ,即r2-b2=16 ③
,即r2-b2=16 ③
