
【题目】已知圆心![]() 为的圆,满足下列条件:圆心
为的圆,满足下列条件:圆心![]() 位于
位于![]() 轴正半轴上,与直线
轴正半轴上,与直线![]() 相切且被轴
相切且被轴![]() 截得的弦长为
截得的弦长为![]() ,圆
,圆![]() 的面积小于13.
的面积小于13.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() .是否存在这样的直线
.是否存在这样的直线![]() ,使得直线
,使得直线![]() 与
与![]() 恰好平行?如果存在,求出
恰好平行?如果存在,求出![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
【答案】(1) ![]() .
.
(2) 不存在这样的直线![]() .
.
【解析】试题分析:(I)用待定系数法即可求得圆C的标准方程;(Ⅱ)首先考虑斜率不存在的情况.当斜率存在时,设直线l:y=kx+3,A(x1,y1),B(x2,y2).l与圆C相交于不同的两点,那么Δ>0.由题设及韦达定理可得k与x1、x2之间关系式,进而求出k的值.若k的值满足Δ>0,则存在;若k的值不满足Δ>0,则不存在.
试题解析:(I)设圆C:(x-a)2+y2=R2(a>0),由题意知
 解得a=1或a=
解得a=1或a=![]() , 3分
, 3分
又∵S=πR2<13,
∴a=1,
∴圆C的标准方程为:(x-1)2+y2=4. 6分
(Ⅱ)当斜率不存在时,直线l为:x=0不满足题意.
当斜率存在时,设直线l:y=kx+3,A(x1,y1),B(x2,y2),
又∵l与圆C相交于不同的两点,
联立![]() 消去y得:(1+k2)x2+(6k-2)x+6=0, 9分
消去y得:(1+k2)x2+(6k-2)x+6=0, 9分
∴Δ=(6k-2)2-24(1+k2)=36k2-6k-5>0,
解得![]() 或
或![]() .
.
x1+x2=![]() ,y1+ y2=k(x1+x2)+6=
,y1+ y2=k(x1+x2)+6=![]() ,
,
![]() ,
,![]() ,
,
假设![]() ∥
∥![]() ,则
,则![]() ,
,
∴![]() ,
,
解得![]() ,假设不成立.
,假设不成立.
∴不存在这样的直线l. 13分


科目:高中数学 来源: 题型:
【题目】如图所示,某街道居委会拟在![]() 地段的居民楼正南方向的空白地段
地段的居民楼正南方向的空白地段![]() 上建一个活动中心,其中
上建一个活动中心,其中![]() 米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形
米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形![]() ,上部分是以
,上部分是以![]() 为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长
为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长![]() 不超过
不超过![]() 米,其中该太阳光线与水平线的夹角
米,其中该太阳光线与水平线的夹角![]() 满足
满足![]() .
.

(1)若设计![]() 米,
米,![]() 米,问能否保证上述采光要求?
米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计![]() 与
与![]() 的长度,可使得活动中心的截面面积最大?(注:计算中
的长度,可使得活动中心的截面面积最大?(注:计算中![]() 取3)
取3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动,在本次海选中有合格和不合格两个等级.若海选合格记1分,海选不合格记0分.假设甲、乙、丙海选合格的概率分别为![]() ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的.
(1)求在这次海选中,这三名音乐爱好者至少有一名海选合格的概率;
(2)记在这次海选中,甲、乙、丙三名音乐爱好者所得分之和为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水是地球上宝贵的资源,由于介个比较便宜在很多不缺水的城市居民经常无节制的使用水资源造成严重的资源浪费.某市政府为了提倡低碳环保的生活理念鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[1,1.5),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图. 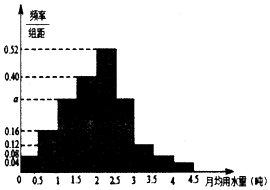
(1)若全市居民中月均用水量不低于3吨的人数为3.6万,试估计全市有多少居民?并说明理由;
(2)若该市政府拟采取分层抽样的方法在用水量吨数为[1,1.5)和[1.5,2)之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设X为用水量吨数在[1,1.5)中的获奖的家庭数,Y为用水量吨数在[1.5,2)中的获奖家庭数,记随机变量Z=|X﹣Y|,求Z的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为了对教师教学水平和教师管理水平进行评价,从该校学生中选出300人进行统计.其中对教师教学水平给出好评的学生人数为总数的![]() ,对教师管理水平给出好评的学生人数为总数的
,对教师管理水平给出好评的学生人数为总数的![]() ,其中对教师教学水平和教师管理水平都给出好评的有120人.
,其中对教师教学水平和教师管理水平都给出好评的有120人.
(1)填写教师教学水平和教师管理水平评价的![]() 列联表:
列联表:
对教师管理水平好评 | 对教师管理水平不满意 | 合计 | |
对教师教学水平好评 | |||
对教师教学水平不满意 | |||
合计 |
请问是否可以在犯错误概率不超过0.001的前提下,认为教师教学水平好评与教师管理水平好评有关?
(2)若将频率视为概率,有4人参与了此次评价,设对教师教学水平和教师管理水平全好评的人数为随机变量![]() .
.
①求对教师教学水平和教师管理水平全好评的人数![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②求![]() 的数学期望和方差.
的数学期望和方差.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取100名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子停下所需的距离),无酒状态与酒后状态下的实验数据分别列于表1和表2.
表1:
停车距离 |
|
|
|
|
|
频数 | 26 | 40 | 24 | 8 | 2 |
表2:
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 |
平均停车距离 | 30 | 50 | 60 | 70 | 90 |
请根据表1,表2回答以下问题.
(1)根据表1估计驾驶员无酒状态下停车距离的平均数;
(2)根据最小二乘法,由表2的数据计算![]() 关于
关于![]() 的回归方程.
的回归方程.![]()
(3)该测试团队认为:驾驶员酒后驾车的“平均停车距离”![]() 大于(1)中无酒状态下的停车距离平均数的3倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?参考公式:
大于(1)中无酒状态下的停车距离平均数的3倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?参考公式:

 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 有两个面平行,其余各面都是四边形的几何体叫棱柱
B. 有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱
C. 用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台
D. 有两个面平行,其余各面都是平行四边形的几何体叫棱柱
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com