
 、
、 、
、 ,各项测试时间间隔恰当,每次测试互不影响.
,各项测试时间间隔恰当,每次测试互不影响.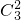 =3种方法
=3种方法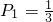 ;
;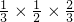 +
+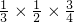 +
+ =
=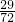 ;
; (
(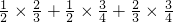 )+
)+ (
(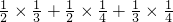 )=
)=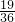
 ,
,| X | 2 | 3 |
| P | 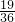 |  |
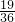 +3×
+3× =
= .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
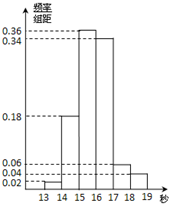 某学校为了解该校1200名男生的百米成绩(单位:秒),随机选择了50名学生进行调查.如图是这50名学生百米成绩的频率分布直方图.根据样本的频率分布,估计这1200名学生中成绩在[13,15](单位:秒)内的人数大约是
某学校为了解该校1200名男生的百米成绩(单位:秒),随机选择了50名学生进行调查.如图是这50名学生百米成绩的频率分布直方图.根据样本的频率分布,估计这1200名学生中成绩在[13,15](单位:秒)内的人数大约是查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:山东省东营市2012届高三一模(3月)数学理科试题 题型:044
某学校为调查了解学生体能状况,决定对高三学生进行一次体育达标测试,具体测试项目有100米跑、立定跳远、掷实心球.测试规定如下:
①三个测试项目中有两项测试成绩合格即可认定为体育达标;
②测试时要求考生先从三个项目中随机抽取两个进行测试,若抽取的两个项目测试都合格或都不合格时,不再参加第三个项目的测试;若抽取的两个项目只有一项合格,则必须参加第三项测试.
已知甲同学跑、跳、掷三个项目测试合格的概率分别是![]() 、
、![]() 、
、![]() ,各项测试时间间隔恰当,每次测试互不影响.
,各项测试时间间隔恰当,每次测试互不影响.
(Ⅰ)求甲同学恰好先抽取跳、掷两个项目进行测试的概率;
(Ⅱ)求甲同学经过两个项目测试就能达标的概率;
(Ⅲ)若甲按规定完成测试,参加测试项目个数为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源:2012年山东省潍坊市、莱芜市、菏泽市、东营市高考数学一模试卷(理科)(解析版) 题型:解答题
 、
、 、
、 ,各项测试时间间隔恰当,每次测试互不影响.
,各项测试时间间隔恰当,每次测试互不影响.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com