
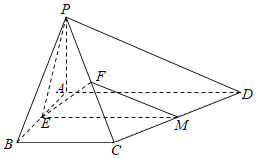
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=∠BAD=90°,AD>BC.E,F分别为棱AB,PC上的点.

(1)求证:平面AFD⊥平面PAB;
(2)若点E满足![]() ,当F满足什么条件时,EF∥平面PAD?请给出证明.
,当F满足什么条件时,EF∥平面PAD?请给出证明.
【答案】(1)见解析(2)当![]() 时,EF∥平面PAD.见解析
时,EF∥平面PAD.见解析
【解析】
(1)只要证AD⊥平面PAB即可,已有AD⊥AB,再由已知线面垂直又得PA⊥AD,从而可证结论成立;
(2)过E作EM∥AD交CD于点M,只要再有![]() ,就有
,就有![]() 都与平面
都与平面![]() 平行,从而得EF∥平面PAD.根据平行线的性质应该有
平行,从而得EF∥平面PAD.根据平行线的性质应该有![]() 即可上面所说的平行.
即可上面所说的平行.
(1)证明:∵∠BAD=90°,∴AD⊥AB.
∵PA⊥平面ABCD,∴PA⊥AD.∴AD⊥平面PAB.
又∵AD平面AFD,
∴平面AFD⊥平面PAB.
(2)过E作EM∥AD交CD于点M,
∵BC∥,![]() ,∴
,∴![]() .
.
过M作MF∥PD,交PC于F,则![]() ,
,
∵EF∥PD,EM平面PAD,PD平面PAD,
∴EM∥平面PAD,
∵MF∥PD,MF平面PAD,PD平面PAD,
∴MF∥平面PAD.
∴平面EFM∥平面PAD,又EF平面EFM,
∴EF∥平面PAD.
∴当![]() 时,EF∥平面PAD.
时,EF∥平面PAD.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知抛物线C的方程C:y2="2" p x(p>0)过点A(1,-2).
(I)求抛物线C的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于![]() ?若存在,求出直线l的方程;若不存在,说明理由。
?若存在,求出直线l的方程;若不存在,说明理由。
【答案】(I)抛物线C的方程为![]() ,其准线方程为
,其准线方程为![]() (II)符合题意的直线l 存在,其方程为2x+y-1 =0.
(II)符合题意的直线l 存在,其方程为2x+y-1 =0.
【解析】
试题(Ⅰ)求抛物线标准方程,一般利用待定系数法,只需一个独立条件确定p的值:(-2)2=2p·1,所以p=2.再由抛物线方程确定其准线方程:![]() ,(Ⅱ)由题意设
,(Ⅱ)由题意设![]() :
:![]() ,先由直线OA与
,先由直线OA与![]() 的距离等于
的距离等于![]() 根据两条平行线距离公式得:
根据两条平行线距离公式得:![]() 解得
解得![]() ,再根据直线
,再根据直线![]() 与抛物线C有公共点确定
与抛物线C有公共点确定![]()
试题解析:解 (1)将(1,-2)代入y2=2px,得(-2)2=2p·1,
所以p=2.
故所求的抛物线C的方程为![]()
其准线方程为![]() .
.
(2)假设存在符合题意的直线![]() ,
,
其方程为![]() .
.
由![]() 得
得![]() .
.
因为直线![]() 与抛物线C有公共点,
与抛物线C有公共点,
所以Δ=4+8t≥0,解得![]() .
.
另一方面,由直线OA到![]() 的距离
的距离![]()
可得![]() ,解得
,解得![]() .
.
因为-1[-![]() ,+∞),1∈[-
,+∞),1∈[-![]() ,+∞),
,+∞),
所以符合题意的直线![]() 存在,其方程为
存在,其方程为![]() .
.
考点:抛物线方程,直线与抛物线位置关系
【名师点睛】求抛物线的标准方程的方法及流程
(1)方法:求抛物线的标准方程常用待定系数法,因为未知数只有p,所以只需一个条件确定p值即可.
(2)流程:因为抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量.
提醒:求标准方程要先确定形式,必要时要进行分类讨论,标准方程有时可设为y2=mx或x2=my(m≠0).
【题型】解答题
【结束】
22
【题目】已知椭圆![]() :
:![]() 的左右焦点与其短轴的一个端点是正三角形的三个顶点,点
的左右焦点与其短轴的一个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过椭圆左焦点
过椭圆左焦点![]() 交椭圆于
交椭圆于![]() ,
,![]() 为椭圆短轴的上顶点,当直线
为椭圆短轴的上顶点,当直线![]() 时,求
时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() 是R上的奇函数.
是R上的奇函数.
(1)求a,b的值;
(2)判断并证明f(x)的单调性;
(3)若对任意实数x,不等式f[f(x)﹣m]![]() 0恒成立,求m的取值范围.
0恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月22日是第50个世界地球日,半个世纪以来,这一呼吁热爱地球环境的运动已经演变为席卷全球的绿色风暴,让越来越多的人认识到保护环境、珍惜自然对人类未来的重要性.今年,自然资源部地球日的主题是“珍爱美丽地球,守护自然资源”.某中学举办了以“珍爱美地球,守护自然资源”为主题的知识竞赛.赛后从该校高一和高二年级的参赛者中随机抽取100人,将他们的竞赛成绩分为7组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到如下频率分布表:

现规定,“竞赛成绩≥80分”为“优秀”“竞赛成绩<80分”为“非优秀”
(Ⅰ)请将下面的2×2列联表补充完整;
优秀 | 非优秀 | 合计 | |
高一 | 50 | ||
高二 | 15 | ||
合计 | 100 |
(Ⅱ)判断是否有99%的把握认为“竞赛成绩与年级有关”?
附:独立性检验界值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,点
,点![]() ,直线
,直线![]() .
.

(1)求与圆![]() 相切,且与直线
相切,且与直线![]() 垂直的直线方程;
垂直的直线方程;
(2)在直线![]() 上(
上(![]() 为坐标原点),存在定点
为坐标原点),存在定点![]() (不同于点
(不同于点![]() ),满足:对于圆
),满足:对于圆![]() 上的任一点
上的任一点![]() ,都有
,都有![]() 为一常数,试求出所有满足条件的点
为一常数,试求出所有满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com