
【题目】已知函数![]() (
(![]() ).
).
(1)若![]() ,求曲线
,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若对任意![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)先根据导数几何意义得切线斜率为![]() ,再根据点斜式写切线方程(2)先将不等式恒成立转化为函数最值:
,再根据点斜式写切线方程(2)先将不等式恒成立转化为函数最值: 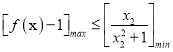 ,再利用导数求函数
,再利用导数求函数![]() 最小值为
最小值为![]() ;根据
;根据![]() 导函数零点
导函数零点![]() ,
, ![]() ,分类讨论,确定导函数符号,进而确定单调性,最后由单调性确定最值取法,解对应不等式可得实数
,分类讨论,确定导函数符号,进而确定单调性,最后由单调性确定最值取法,解对应不等式可得实数![]() 的取值范围.
的取值范围.
试题解析:(1)依题意, ![]() ,
, ![]() ,故
,故![]() ,
,
又![]() ,故所求切线方程为
,故所求切线方程为![]() ,即
,即![]() ;
;
(2)令![]() ,故函数
,故函数![]() 的定义域为
的定义域为![]() ,
, 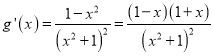 .
.
当![]() 变化时,
变化时, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| 单调减 | 单调增 | 单调减 |
因为![]() ,
, ![]() ,所以
,所以![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ;
;
因为![]() . 因为
. 因为![]() ,令
,令![]() 得,
得, ![]() ,
, ![]() .
.
(ⅰ)当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,所以函数
上单调递增,所以函数![]() .由
.由![]() 得,
得, ![]() ,所以
,所以![]() .
.
(ⅱ)当![]() ,即
,即![]() 时, 在
时, 在![]() 上
上![]() ,在
,在![]() 上
上![]() ,
,
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,所以
上单调递减,所以![]() ,由
,由![]() 得,
得, ![]() ,所以
,所以![]() .
.
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:
高峰时间段用电价格表 | 低谷时间段用电价格表 | ||
高峰月用 电量(单 位:千瓦时) | 高峰电价 (单位:元/ 千瓦时) | 低谷月用 电量(单位: 千瓦时) | 低谷电价 (单位:元/ 千瓦时) |
50及以下 的部分 | 0.568 | 50及以下 的部分 | 0.288 |
超过 50 至 200 的部分 | 0.598 | 超过 50 至 200 的部分 | 0.318 |
超过200 的部分 | 0.668 | 超过 200 的部分 | 0.388 |
若某家庭5月份的高峰时间段用电量为 200 千瓦时,低谷时间段用电量为 100 千瓦时,则按这种计费方式该家庭本月应付的电费为____________元.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(![]() )x.
)x.
(Ⅰ)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值g(a);
(Ⅱ)在(Ⅰ)的条件下,是否存在实数m>n>3,使得g(x)的定义域为[n,m],值域为[n2,m2]?若存在,求出m、n的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】信息科技的进步和互联网商业模式的兴起,全方位地改变了大家金融消费的习惯和金融交易模式,现在银行的大部分业务都可以通过智能终端设备完成,多家银行职员人数在悄然减少.某银行现有职员320人,平均每人每年可创利20万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.2万元,但银行需付下岗职员每人每年6万元的生活费,并且该银行正常运转所需人数不得小于现有职员的![]() ,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数
,若存在实数![]() ,使
,使 ![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.
的不动点.
(1)当![]() 时,求
时,求![]() 的不动点;
的不动点;
(2)若对于任意的实数![]() 函数
函数 ![]() 恒有两个相异的不动点,求实数
恒有两个相异的不动点,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() 的图象上
的图象上![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且直线
的不动点,且直线![]() 是线段
是线段![]() 的垂直平分线,求实数
的垂直平分线,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域为![]() 的函数
的函数![]() 同时满足以下三条:
同时满足以下三条:
(ⅰ)对任意的![]() 总有
总有![]() (ⅱ)
(ⅱ)![]()
(ⅲ)若![]() 则有
则有![]() 就称
就称![]() 为“A函数”,下列定义在
为“A函数”,下列定义在![]() 的函数中为“A函数”的有_______________
的函数中为“A函数”的有_______________
①![]() ;②
;②![]() ③
③![]() ④
④![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 且点(4,2)在函数f(x)的图象上.
且点(4,2)在函数f(x)的图象上.
(1)求函数f(x)的解析式,并在图中的直角坐标系中画出函数f(x)的图象;
(2)求不等式f(x)<1的解集;
(3)若方程f(x)-2m=0有两个不相等的实数根,求实数m的取值范围.
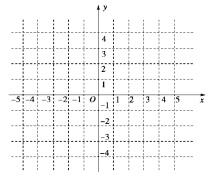
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com