练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在数列{an}中，a1＝1，且Sn，Sn＋1,2S1成等差数列(Sn表示数列{an}的前n项和)，则S2，S3，S4分别为__________________，猜想Sn＝________.

    ，， 

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    对大于或等于2的正整数的幂运算有如下分解方式：
         …
         …
    根据上述分解规律，若，的分解中最小的正整数是21，则    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    观察下列不等式
    1+<,
    1++<,
    1+++<,
    …
    照此规律,第五个不等式为　　　　　　　　.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    观察下列等式
    1＝1
    2＋3＋4＝9
    3＋4＋5＋6＋7＝25
    4＋5＋6＋7＋8＋9＋10＝49
    …
    照此规律，第n个等式为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    挪威数学家阿贝尔曾经根据阶梯形图形的两种不同分割（如下图），利用它们的面积关系发现了一个重要的恒等式——阿贝尔公式：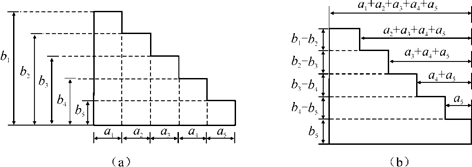

    a1b1＋a2b2＋a3b3＋…＋anbn＝L1(b1－b2)＋L2(b2－b3)＋L3(b3－b4)＋…＋Ln－1(bn－1－bn)＋Lnbn，其中L1＝a1，则
    （Ⅰ）L3＝           ；
    （Ⅱ）Ln＝                 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    （2013•湖北）古希腊毕达哥拉斯学派的数学家研究过各种多边形数，如三角形数1，3，6，10，…，第n个三角形数为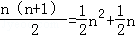．记第n个k边形数为N（n，k）（k≥3），以下列出了部分k边形数中第n个数的表达式：
    三角形数，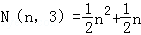
    正方形数N（n，4）=n2，
    五边形数，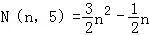
    六边形数N（n，6）=2n2﹣n，
    …
    可以推测N（n，k）的表达式，由此计算N（10，24）=　_________　．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    现有一个关于平面图形的命题：如图所示，同一个平面内有两个边长都是a的正方形，其中一个的某顶点在另一个的中心，则这两个正方形重叠部分的面积恒为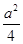.类比到空间，有两个棱长均为a的正方体，其中一个的某顶点在另一个的中心，则这两个正方体重叠部分的体积恒为________．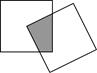

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    在平面几何中，△ABC的内角平分线CE分AB所成线段的比为，把这个结论类比到空间：在三棱锥A－BCD中(如图所示)，平面DEC平分二面角A－CD－B且与AB相交于E，则得到的类比的结论是________．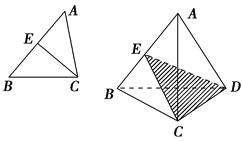

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    用数学归纳法证明:(n+1)+ (n+2)+…+(n+n)=(n∈N*)的第二步中,当n=k+1时等式左边与n=k时的等式左边的差等于　　　.

    查看答案和解析>>

    同步练习册答案