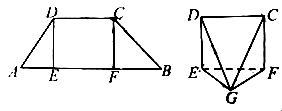已知
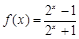
.
(1)讨论
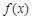
的奇偶性;
(2)讨论
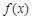
的单调性.
本试题主要考查了函数的奇偶性和单调性的运用。
(1)
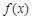
的定义域为
R.
∵
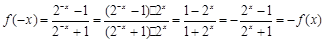
. …………………………4分
∴
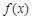
为奇函数. …………………………6分
(2)设任意
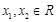
,且
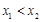
,则

.…………………………9分
由于
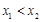
,从而
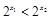
,即
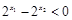
.
∴
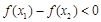
,即
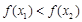
. ∴
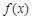
为增函数. …………………12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
如图,梯形
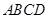
中,
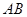
∥
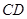
,
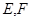
是线段
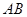
上的两点,且
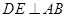
,
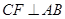
,
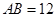
,
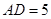
,
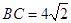
,
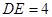
.现将△
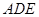
,△
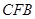
分别沿
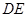
,
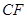
折起,使两点
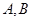
重合于点
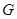
,得到多面体
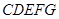
(1)求证:平面
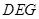
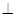
平面
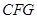
;(2)求多面体
的体积
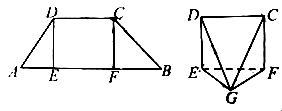
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设f(X)是定义在R上周期为4的奇函数,当
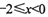
时,
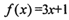
,则f(5)的值为
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知定义域为R的函数
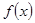
是奇函数,当
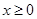
时,

|
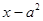
|-
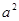
,且对
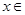
R,恒有
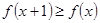
,则实数
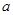
的取值范围为
| A.[0,2] | B.[-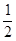 , ,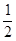 ] ] | C.[-1,1] | D.[-2,0] |
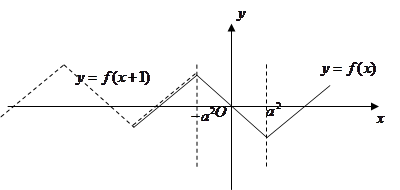
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知
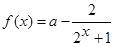
是定义在R上奇函数,则
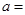
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设函数
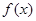
(x∈R)为奇函数,
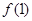
=
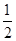
,
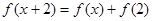
,则
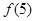
=( )
| A.0 | B.1 | C. | D.5 |
查看答案和解析>>

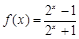 .
. 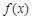 的奇偶性;
的奇偶性; 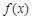 的单调性.
的单调性. 阅读快车系列答案
阅读快车系列答案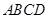 中,
中,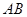 ∥
∥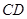 ,
,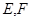 是线段
是线段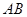 上的两点,且
上的两点,且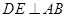 ,
,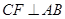 ,
,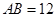 ,
,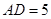 ,
,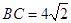 ,
,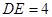 .现将△
.现将△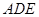 ,△
,△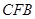 分别沿
分别沿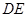 ,
,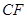 折起,使两点
折起,使两点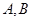 重合于点
重合于点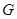 ,得到多面体
,得到多面体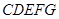 (1)求证:平面
(1)求证:平面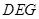
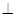 平面
平面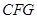 ;(2)求多面体
;(2)求多面体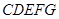 的体积
的体积