
【题目】一座圆拱桥,当水面在如图所示位置时,拱顶离水面2米,水面宽12米,当水面下降1米后,水面宽多少米?
![]()
【答案】2![]()
【解析】试题分析; 建立适当的直角坐标系,得到相关各点的坐标,通过设圆的半径,可得圆的方程,然后将点的坐标代入确定圆的方程,设当水面下降1米后可设![]() 的坐标为
的坐标为![]() 根据点在圆上,可求得
根据点在圆上,可求得![]() 的值,从而得到问题的结果.
的值,从而得到问题的结果.
试题解析;以圆拱顶点为原点,以过圆拱顶点的竖直直线为y轴,建立如图所示的平面直角坐标系.
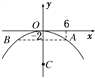
设圆心为C,水面所在弦的端点为A,B,则由已知可得A(6,-2),
设圆的半径长为r,则C(0,-r),即圆的方程为x2+(y+r)2=r2.将点A的坐标代入上述方程可得r=10,所以圆的方程为x2+(y+10)2=100.
当水面下降1米后,可设A′(x0,-3)(x0>0),代入x2+(y+10)2=100,解得2x0=2![]() ,即当水面下降1米后,水面宽2
,即当水面下降1米后,水面宽2![]() 米.
米.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
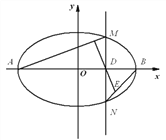
【题目】已知椭圆![]() 的两个顶点分别为
的两个顶点分别为![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)点![]() 为
为![]() 轴上一点,过
轴上一点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于不同的两点
于不同的两点![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .求
.求![]() 与
与![]() 的面积之比.
的面积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某DVD光盘销售部每天的房租、人员工资等固定成本为300元,每张DVD光盘的进价是6元,销售单价与日均销售量的关系如表所示:
销售单价(元) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
日均销售量(张) | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
(1)请根据以上数据作出分析,写出日均销售量P(x)(张)关于销售单价x(元)的函数关系式,并写出其定义域;
(2)问这个销售部销售的DVD光盘销售单价定为多少时才能使日均销售利润最大?最大销售利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C是△ABC的三个内角,向量m=(-1, ![]() ),n=(cosA,sinA),且m·n=1.
),n=(cosA,sinA),且m·n=1.
(1)求角A;
(2)若![]() =-3,求tanC.
=-3,求tanC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,求数列
,求数列![]() 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
思路1:先设![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出![]() _________,
_________, ![]() __________,
__________, ![]() _________.
_________.
猜想: ![]() _______.
_______.
然后用数学归纳法证明.证明过程如下:
①当![]() 时,________________,猜想成立
时,________________,猜想成立
②假设![]() (
(![]() N*)时,猜想成立,即
N*)时,猜想成立,即![]() _______.
_______.
那么,当![]() 时,由已知
时,由已知![]() ,得
,得![]() _________.
_________.
又![]() ,两式相减并化简,得
,两式相减并化简,得![]() _____________(用含
_____________(用含![]() 的代数式表示).
的代数式表示).
所以,当![]() 时,猜想也成立.
时,猜想也成立.
根据①和②,可知猜想对任何![]() N*都成立.
N*都成立.
思路2:先设![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出![]() _____________.
_____________.
由已知![]() ,写出
,写出![]() 与
与![]() 的关系式:
的关系式: ![]() _____________________,
_____________________,
两式相减,得![]() 与
与![]() 的递推关系式:
的递推关系式: ![]() ____________________.
____________________.
整理: ![]() ____________.
____________.
发现:数列![]() 是首项为________,公比为_______的等比数列.
是首项为________,公比为_______的等比数列.
得出:数列![]() 的通项公式
的通项公式![]() ____,进而得到
____,进而得到![]() ____________.
____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形ABCD和正方形ABEF的边长都是1,并且平面ABCD⊥平面ABEF,点M在AC上移动,点N在BF上移动.若|CM|=|BN|=a(0<a<![]() ).
).
(1)求MN的长度;
(2)当a为何值时,MN的长度最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)求f(2)与f![]() , f(3)与f
, f(3)与f![]() ;
;
(2)由(1)中求得结果,你能发现f(x)与f![]() 有什么关系?并证明你的发现;
有什么关系?并证明你的发现;
(3)求f(1)+f(2)+f(3)+…+f(2013)+f![]() +f
+f![]() +…+f
+…+f![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() ,曲线
,曲线![]() :
: ![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线![]() ,
, ![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ,
, ![]() )分别交
)分别交![]() ,
, ![]() 于
于![]() ,
, ![]() 两点,当
两点,当![]() 取何值时,
取何值时, ![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为自然对数的底数),
为自然对数的底数),![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,求证:
时,求证:![]() ;
;
(Ⅱ)是否存在正整数![]() ,使得
,使得![]() 对一切
对一切![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com