
【题目】已知函数f(x)=﹣x3+ax2+1,(a∈R).
(1)若f(x)图象上横坐标为1的点处存在垂直于y轴的切线,求a的值;
(2)若f(x)在区间(﹣1,2)内有两个不同的极值点,求a取值范围;
(3)当a=1时,是否存在实数m,使得函数g(x)=x4﹣5x3+(2﹣m)x2+1的图象于函数f(x)的图象恰有三个不同的交点,若存在,试求出实数m的值;若不存在,说明理由.
【答案】
(1)解:依题意,f′(1)=0
∵f′(x)=﹣3x2+2ax
﹣3(1)2+2a1=0,
∴a= ![]()
(2)解:若f(x)在区间(﹣1,2)内有两个不同的极值点,
则方程f′(x)=﹣3x2+2ax=0在区间(﹣1,2)内有两个不同的实根,
∴△>0,f′(﹣1)<0,f′(2)<0,﹣1< ![]() <2,
<2,
解得:﹣ ![]() <a<3且a≠0
<a<3且a≠0
但a=0时,f(x)=﹣x3+1无极值点,
∴a的取值范围为(﹣ ![]() ,0)∪(0,3)
,0)∪(0,3)
(3)解:a=1时,f(x)=﹣x3+x2+1,
要使函数f(x)与g(x)=x4﹣5x3+(2﹣m)x2+1的图象恰有三个交点,
等价于方程﹣x3+x2+1=x4﹣5x3+(2﹣m)x2+1,
即方程x2(x2﹣4x+1﹣m)=0恰有三个不同的实根.
∵x=0是一个根,
∴应使方程x2﹣4x+1﹣m=0有两个非零的不等实根,
由△=16﹣4(1﹣m)>0,1﹣m≠0,解得m>﹣3,m≠1,
∴存在m∈(﹣3,1)∪(1,+∞),
使用函数f(x)与g(x)=x4﹣5x3+(2﹣m)x2+1的图象恰有三个交点
【解析】(1)先求出函数的导数,再由f′(1)=0求解a.(2)将“f(x)在区间(﹣1,2)内有两个不同的极值点”转化为“方程f′(x)=0在区间(﹣1,2)内有两个不同的实根”,用△>0求解.(3)a=1,“要使函数f(x)与g(x)=x4﹣5x3+(2﹣m)x2+1的图象恰有三个交点”即为“方程x2(x2﹣4x+1m)=0恰有三个不同的实根”.因为x=0是一个根,所以方程x2﹣4x+1﹣m=0应有两个非零的不等实根,再用判别式求解.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】给出下列说法:
①集合A={x∈Z|x=2k﹣1,k∈Z}与集合B={x∈z|x=2k+3,k∈Z}是相等集合;
②若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];
③函数y= ![]() 的单调减区间是(﹣∞,0)∪(0,+∞);
的单调减区间是(﹣∞,0)∪(0,+∞);
④不存在实数m,使f(x)=x2+mx+1为奇函数;
⑤若f(x+y)=f(x)f(y),且f(1)=2,则 ![]() +
+ ![]() +…+
+…+ ![]() =2016.
=2016.
其中正确说法的序号是( )
A.①②③
B.②③④
C.①③⑤
D.①④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图为某市2017年2月28天的日空气质量指数折线图.
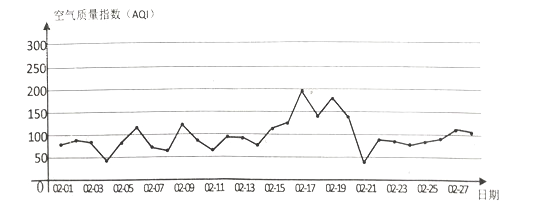
由中国空气质量在线监测分析平台提供的空气质量指数标准如下:

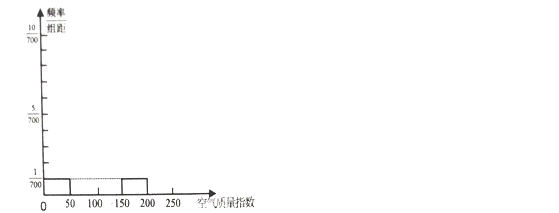
(1)请根据所给的折线图补全下方的频率分布直方图(并用铅笔涂黑矩形区域),并估算该市2月份空气质量指数监测数据的平均数(保留小数点后一位);
(2)研究人员发现,空气质量指数测评中![]() 与燃烧排放的
与燃烧排放的![]() 两个项目存在线性相关关系,以
两个项目存在线性相关关系,以![]() 为单位,下表给出
为单位,下表给出![]() 与
与![]() 的相关数据:
的相关数据:

求![]() 关于
关于![]() 的回归方程,并估计当
的回归方程,并估计当![]() 排放量是
排放量是![]() 时,
时, ![]() 的值.
的值.
(用最小二乘法求回归方程的系数是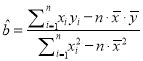 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=(|x﹣a2|+|x﹣2a2|﹣3a2),若对于任意x∈R,都有f(x﹣2)≤f(x),则实数a的取值范围是( )
A.[﹣ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com