
【题目】已知函数![]() .
.
(1)证明:函数![]() 在区间
在区间![]() 上存在唯一的极小值点;
上存在唯一的极小值点;
(2)证明:函数![]() 有且仅有两个零点.
有且仅有两个零点.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)由导函数解析式可确定导函数在![]() 上单调递增;利用零点存在性定理可知存在唯一
上单调递增;利用零点存在性定理可知存在唯一![]() 使得
使得![]() ,由此可确定
,由此可确定![]() 单调性,从而得到结论;
单调性,从而得到结论;
(2)①当![]() 时,由
时,由![]() 可知
可知![]() 单调递减,由此可确定
单调递减,由此可确定![]() 为
为![]() 的一个零点;②当
的一个零点;②当![]() 时,由零点存在定理和(1)中
时,由零点存在定理和(1)中![]() 单调性,可确定
单调性,可确定![]() 存在唯一的零点;③当
存在唯一的零点;③当![]() 时,令
时,令![]() ,由
,由![]() 可确定
可确定![]() 单调递增,则
单调递增,则![]() ,由此可确定
,由此可确定![]() ,进而得到
,进而得到![]() 无零点;综合三种情况可得结论.
无零点;综合三种情况可得结论.
(1)![]()
当![]() 时,函数
时,函数![]() 和
和![]() 单调递减
单调递减
![]() 函数
函数![]() 单调递增
单调递增
又由![]() ,
,![]()
故存在唯一![]() 使得
使得![]()
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 当
当![]() 时,函数
时,函数![]() 单调递减;当
单调递减;当![]() 时,函数
时,函数![]() 单调递增
单调递增
故函数![]() 在区间
在区间![]() 上存在唯一的极小值点
上存在唯一的极小值点
(2)①当![]() 时,由
时,由![]()
又由![]() ,
,![]() ,可得
,可得![]() ,故在区间
,故在区间![]() 上函数
上函数![]() 单调递减
单调递减
又由![]() ,故有
,故有![]()
可得此时函数![]() 的零点为
的零点为![]()
②当![]() 时,由
时,由![]() ,
,![]()
![]()
![]()
由(1)可知,此时函数![]() 在区间
在区间![]() 上有唯一的零点;
上有唯一的零点;
③当![]() 时,令
时,令![]()
则![]() ,故此时函数
,故此时函数![]() 单调递增
单调递增
有![]()
又由![]() ,故对
,故对![]() ,有
,有![]()
所以在区间![]() 上函数
上函数![]() 没有零点
没有零点
综上所述,函数![]() 有且仅有两个零点
有且仅有两个零点


科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 时,有极值,求
时,有极值,求![]() 的值;
的值;
(2)在直线![]() 上是否存在点
上是否存在点![]() ,使得过点
,使得过点![]() 至少有两条直线与曲线
至少有两条直线与曲线![]() 相切?若存在,求出
相切?若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】至![]() 年底,我国发明专利申请量已经连续
年底,我国发明专利申请量已经连续![]() 年位居世界首位,下表是我国
年位居世界首位,下表是我国![]() 年至
年至![]() 年发明专利申请量以及相关数据.
年发明专利申请量以及相关数据.
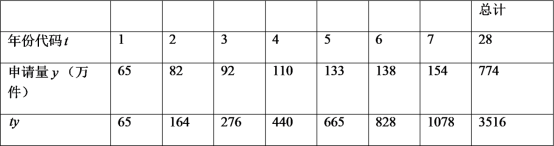
注:年份代码![]() ~
~![]() 分别表示
分别表示![]() ~
~![]() .
.
(1)可以看出申请量每年都在增加,请问这几年中哪一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到
的回归直线方程(精确到![]() ),并预测我国发明专利申请量突破
),并预测我国发明专利申请量突破![]() 万件的年份.
万件的年份.
参考公式:回归直线的斜率和截距的最小二乘法估计分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,动点E到定点![]() 和定直线
和定直线![]() 的距离相等.
的距离相等.
(1)求动点E的轨迹C的方程;
(2)设动直线![]()
![]() 与曲线C有唯一的公共点P,与直线
与曲线C有唯一的公共点P,与直线![]() 相交于点Q,若
相交于点Q,若![]() ,求证:点M的轨迹恒过定点
,求证:点M的轨迹恒过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )

①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近来天气变化无常,陡然升温、降温幅度大于![]() 的天气现象出现增多.陡然降温幅度大于
的天气现象出现增多.陡然降温幅度大于![]() 容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的
容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的![]() 名幼儿进行调查,得到了如下的列联表,若在全部
名幼儿进行调查,得到了如下的列联表,若在全部![]() 名幼儿中随机抽取
名幼儿中随机抽取![]() 人,抽到患伤风感冒疾病的幼儿的概率为
人,抽到患伤风感冒疾病的幼儿的概率为![]() ,
,
(1)请将下面的列联表补充完整;
患伤风感冒疾病 | 不患伤风感冒疾病 | 合计 | |
男 | 25 | ||
女 | 20 | ||
合计 | 100 |
(2)能否在犯错误的概率不超过![]() 的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
(3)已知在患伤风感冒疾病的![]() 名女性幼儿中,有
名女性幼儿中,有![]() 名又患黄痘病.现在从患伤风感冒疾病的
名又患黄痘病.现在从患伤风感冒疾病的![]() 名女性中,选出
名女性中,选出![]() 名进行其他方面的排查,记选出患黄痘病的女性人数为
名进行其他方面的排查,记选出患黄痘病的女性人数为![]() ,求
,求![]() 的分布列以及数学期望.下面的临界值表供参考:
的分布列以及数学期望.下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: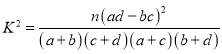 ,其中
,其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com