本试题主要是考查了几何概型的运用。对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果。
由题意知本题是一个几何概型,∵a∈[0,2],∴f'(x)=3x
2+a≥0,∴f(x)是增函数若f(x)在[-1,1]有且仅有一个零点,则f(-1)•f(1)≤0∴(-1-a-b)(1+a-b)≤0,即(1+a+b)(1+a-b)≥0由线性规划内容知全部事件的面积为2×2=4,满足条件的面积4-
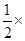
×1×1=
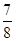
,故选D.
解决该试题的关键是根据所给的条件很容易做出试验发生包含的事件对应的面积,而满足条件的事件是函数f(x)=x
3+ax-b在区间[-1,1]上有且仅有一个零点,求出导函数,看出函数是一个增函数,有零点等价于在自变量区间的两个端点处函数值符号相反,得到条件,做出面积,根据几何概型概率公式得到结果。

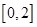 上任取两个实数
上任取两个实数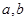 ,则函数
,则函数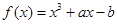 在区间
在区间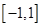 上有且只有一个零点的概率是
上有且只有一个零点的概率是
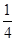
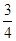
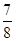
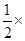 ×1×1=
×1×1=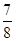 ,故选D.
,故选D.
