
【题目】已知向量 ![]() =(cosωx,sinωx),
=(cosωx,sinωx), ![]() =(cosωx,
=(cosωx, ![]() cosωx),其中ω>0,设函数f(x)=
cosωx),其中ω>0,设函数f(x)= ![]()
![]() .
.
(1)若函数f(x)的最小正周期是π,求函数f(x)的单调递增区间;
(2)若函数f(x)的图象的一个对称中心的横坐标为 ![]() ,求ω的最小值.
,求ω的最小值.
【答案】
(1)解:f(x)=cos2ωx+ ![]() sinωxcosωx=
sinωxcosωx= ![]() cos2ωx+
cos2ωx+ ![]() sin2ωx+
sin2ωx+ ![]() =sin(2ωx+
=sin(2ωx+ ![]() )+
)+ ![]() .
.
∴T= ![]() =π,ω=1,
=π,ω=1,
∴f(x)=sin(2x+ ![]() )+
)+ ![]() .
.
令﹣ ![]() 2x+
2x+ ![]() ,解得
,解得 ![]() +kπ≤x≤
+kπ≤x≤ ![]() .
.
∴f(x)的单调递增区间是[ ![]() +kπ,
+kπ, ![]() ],k∈Z
],k∈Z
(2)解:∵函数f(x)的图象的一个对称中心的横坐标为 ![]() ,
,
∴sin( ![]() )=0,∴
)=0,∴ ![]() =kπ,解得ω=3k﹣
=kπ,解得ω=3k﹣ ![]() .
.
∵ω>0,∴当k=1时,ω取得最小值 ![]()
【解析】(1)化简f(x),利用周期公式求出ω得出f(x)的解析式,利用正弦函数的单调性列出不等式解出单调增区间;(2)利用正弦函数的性质得出sin( ![]() )=0,解出ω.
)=0,解出ω.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,离心率等于
的中心在原点,离心率等于![]() ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线![]() 的焦点
的焦点
(1)求椭圆![]() 的方程;
的方程;
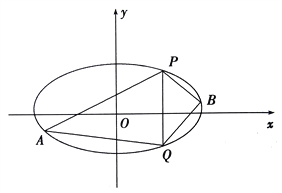
(2)已知![]() 、
、![]() 是椭圆上的两点,
是椭圆上的两点, ![]() ,
, ![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.①若直线
两侧的动点.①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②当![]() ,
, ![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由
的斜率是否为定值,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 且
且![]() ,直线:
,直线: ![]() ,圆
,圆![]() :
:![]()
![]() .
.
(Ⅰ)若![]() ,请判断直线与圆
,请判断直线与圆![]() 的位置关系;
的位置关系;
(Ⅱ)求直线倾斜角![]() 的取值范围;
的取值范围;
(Ⅲ)直线能否将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段圆弧?为什么?
的两段圆弧?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过椭圆![]() :
: ![]() 上一点
上一点![]() 向
向![]() 轴作垂线,垂足为右焦点
轴作垂线,垂足为右焦点![]() ,
, ![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左顶点和上顶点,且
的左顶点和上顶点,且![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,且以
两点,且以![]() 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点![]() .问是否存在一个定圆与动直线
.问是否存在一个定圆与动直线![]() 总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 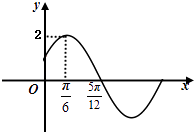
(1)求函数f(x)的解析式;
(2)令g(x)=f(﹣x﹣ ![]() ),求g(x)的单调递增区间.
),求g(x)的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com