
【题目】已知{an}是递增的等差数列,它的前三项的和为﹣3,前三项的积为8.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的前n项和Sn .
【答案】
(1)解:设{an}的公差为d(d>0),依题意, ![]() ,
,
即 ![]() ,解得
,解得 ![]() 或
或 ![]() ,
,
因为d>0,所以 ![]() ,{an}的通项an=﹣7+3n
,{an}的通项an=﹣7+3n
(2)解:由(1)得a1=﹣4,|a1|=4;a2=﹣1,|a2|=1;
当n≥3时,an>0,|an|=an,
所以S1=4,S2=5
当n≥3时,Sn=S2+(a3+…an)=5+[2+…+(﹣7+3n)]
=5+ ![]() ×(n﹣2)
×(n﹣2)
= ![]() n2﹣
n2﹣ ![]() n+10
n+10
综上所述,Sn= 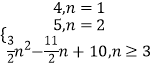
【解析】(1)依题意,解方程组 ![]() 即可求得数列{an}的首项与公差,再利用{an}是递增的等差数列进行取舍,即可求得答案;(2)由(1)得当n≥3时,an>0,|an|=an , 通过对n=1与n=2及n≥3的情况的讨论即可求得Sn .
即可求得数列{an}的首项与公差,再利用{an}是递增的等差数列进行取舍,即可求得答案;(2)由(1)得当n≥3时,an>0,|an|=an , 通过对n=1与n=2及n≥3的情况的讨论即可求得Sn .
【考点精析】本题主要考查了数列的前n项和和等差数列的性质的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系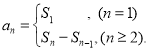 ;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列才能正确解答此题.
;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人玩数字游戏,先由甲任想一个数字记为a,再由乙猜甲刚才想的数字,把乙想的数字记为b,且a,b∈{1,2,3,4,5,6},记ξ=|a﹣b|.
(1)求ξ=1的概率;
(2)若ξ≤1,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,由三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax+1|+|2x﹣1|(a∈R).
(1)当a=1时,求不等式f(x)≥2的解集;
(2)若f(x)≤2x在x∈[![]() ,1]时恒成立,求a的取值范围.
,1]时恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆
是圆![]() 上任意一点,点
上任意一点,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 分别与线段
分别与线段![]() 交于
交于![]() 两点,且
两点,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,设
两点,设![]() 为坐标原点,
为坐标原点, ![]() ,判断
,判断![]() 的面积是否为定值?若是,求出定值,若不是,说明理由.
的面积是否为定值?若是,求出定值,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下关于命题的说法正确的有(选择所有正确命题的序号).
(1)“若![]() ,则函数
,则函数![]() 在其定义域内是减函数”是真命题;
在其定义域内是减函数”是真命题;
(2)命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”;
”;
(3)命题“若![]() 都是偶函数,则
都是偶函数,则![]() 也是偶数”的逆命题为真命题;
也是偶数”的逆命题为真命题;
(4)命题“若![]() ,则
,则![]() ”与命题“若
”与命题“若![]() ,则
,则![]() ”等价.
”等价.
A. (1)(3) B. (2)(3) C. (2)(4) D. (3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现如今,“网购”一词不再新鲜,越来越多的人已经接受并喜欢了这种购物方式,但随之也出现了商品质量不能保证与信誉不好等问题,因此,相关管理部门制定了针对商品质量与服务的评价体系,现从评价系统中选出成功交易200例,并对其评价进行统计:对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)依据题中的数据完成下表,并通过计算说明,能否有99.9%的把握认为“商品好评与服务好评”有关;
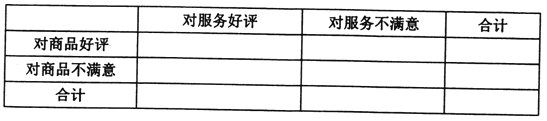
(2)若将频率视为概率,某人在该购物平台上进行了5次购物,设对商品和服务全好评的次数为随机变量![]() ,求
,求![]() 的分布列(概率用算式表示)、数学期望和方差.
的分布列(概率用算式表示)、数学期望和方差.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (a>0且a≠1)是定义在R上的奇函数. (Ⅰ) 求实数a的值;
(a>0且a≠1)是定义在R上的奇函数. (Ⅰ) 求实数a的值;
(Ⅱ) 证明函数f(x)在R上是增函数;
(Ⅲ)当x∈[1,+∞)时,mf(x)≤2x﹣2恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com