
分析 (1)根据函数恒成立,利用参数分离法进行求解即可.
(2)根据函数表达式,转化为点到直线的距离和点到点的距离进行求解即可.
解答 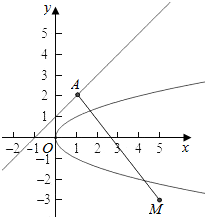 解:(1)若f(x)≥ax2+a对任意的x∈R恒成立,
解:(1)若f(x)≥ax2+a对任意的x∈R恒成立,
即x2-x+1≥ax2+a对任意的x∈R恒成立,
即(1-a)x2-x+1-a≥0恒成立,
若a=1,则不等式等价为-x≥0,则x≤0,不满足条件.
若a≠1,则等价为$\left\{\begin{array}{l}{1-a>0}\\{△=1-4(1-a)^{2}≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a<1}\\{(a-1)^{2}≥\frac{1}{4}}\end{array}\right.$,即a-1≤-$\frac{1}{2}$,即a≤1-$\frac{1}{2}$=$\frac{1}{2}$.
即实数a的取值范围是(-∞,$\frac{1}{2}$].
(2)令y=f(x)+$\sqrt{g(x)}$,则$\frac{y}{\sqrt{2}}$=$\frac{{x}^{2}-x+1}{\sqrt{2}}$+$\sqrt{({x}^{2}-5)^{2}+(x+3)^{2}}$
$\frac{{x}^{2}-x+1}{\sqrt{2}}$表示抛物线x=y2上的动点(x2,x)到直线l:x-y+1=0的距离,$\sqrt{({x}^{2}-5)^{2}+(x+3)^{2}}$表示抛物线x=y2上的动点(x2,x)到点M(5,-3)的距离,
则=$\frac{{x}^{2}-x+1}{\sqrt{2}}$+$\sqrt{({x}^{2}-5)^{2}+(x+3)^{2}}$表示抛物线x=y2上的动点(x2,x)到直线l:x-y+1=0的距离与到点M(5,-3)的距离之和,
则最小值为M到y-x+1=0的距离d=$\frac{|-3-5+1|}{\sqrt{2}}$=$\frac{7}{\sqrt{2}}$=$\frac{7\sqrt{2}}{2}$,
即$\frac{y}{\sqrt{2}}$≥$\frac{7\sqrt{2}}{2}$,即y≥$\frac{7\sqrt{2}}{2}$×$\sqrt{2}$=7,
即M≤7,即M的最大值为7.
点评 本题主要考查不等式恒成立问题,根据条件进行转化是解决本题的关键.综合性较强,难度较大.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
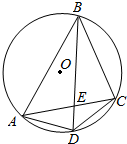 如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于点E.
如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于点E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com