
【题目】已知函数f(x)=![]() ,其中a∈R.
,其中a∈R.
(I)当a=1时,求曲线y=f(x)在原点处的切线方程;
(II)求f(x)的极值.
【答案】(I)2x-y=0; (II)见解析.
【解析】试题分析:(1)求出在原点处的导数值,得斜率,即可求出切线方程;
(2)求出导数,讨论单调性得极值.
试题解析:
(I)解:当a=1时,f(x)=![]() ,f '(x)=-2
,f '(x)=-2 .…………2分
.…………2分
由f '(0)=2,得曲线y=f(x)在原点处的切线方程是2x-y=0.………4分
(II)解:f '(x)=-2![]() . ………6分
. ………6分
①当a=0时,f '(x)=![]() .
.
所以f(x)在(0,+∞)单调递增,(-∞,0)单调递减. ………………7分
当a≠0,f '(x)=-2a .
.
②当a>0时,令f '(x)=0,得x1=-a,x2=![]() ,f(x)与f '(x)的情况如下:
,f(x)与f '(x)的情况如下:
x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
f '(x) | - | 0 | + | 0 | - |
f(x) | ↘ | f(x1) | ↗ | f(x2) | ↘ |
故f(x)的单调减区间是(-∞,-a),(![]() ,+∞);单调增区间是(-a,
,+∞);单调增区间是(-a, ![]() ).
).
f(x)有极小值f(-a)=-1,有极大值f(![]() )=a2 ………10分
)=a2 ………10分
③当a<0时,f(x)与f '(x)的情况如下:
x | (-∞,x2) | x2 | (x2,x1) | x1 | (x1,+∞) |
f '(x) | + | 0 | - | 0 | + |
f(x) | ↗ | f(x2) | ↘ | f(x1) | ↗ |
所以f(x)的单调增区间是(-∞,![]() );单调减区间是(-
);单调减区间是(-![]() ,-a),(-a,+ ∞)。
,-a),(-a,+ ∞)。
f(x)有极小值f(-a)=-1,有极大值f(![]() )=a2 ………………12分
)=a2 ………………12分
综上,a>0时,f(x)在(-∞,-a),(![]() ,+∞)单调递减;在(-a,
,+∞)单调递减;在(-a, ![]() )单调递增.
)单调递增.
a=0时,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减,f(x)有极小值f(-a)=-1,有极大值,f(![]() )=a2;a<0时,f(x)在(-∞,
)=a2;a<0时,f(x)在(-∞, ![]() ),(-a,+∞)单调递增;在(
),(-a,+∞)单调递增;在(![]() ,-a)单调递减,f(x)有极小值f(-a)=-1,有极大值f(
,-a)单调递减,f(x)有极小值f(-a)=-1,有极大值f(![]() )=a2.
)=a2.


科目:高中数学 来源: 题型:
【题目】记![]() 表示
表示![]() 中的最大值,如
中的最大值,如![]() ,已知函数
,已知函数![]() .
.
(1)求函数![]() 在
在![]() 上的值域;
上的值域;
(2)试探讨是否存在实数![]() , 使得
, 使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;
的取值范围;
若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】比较下列各组中两个值的大小 :
(1)ln0.3,ln2; (2)loga3.1,loga5.2(a>0,且a≠1);
(3)log30.2,log40.2; (4)log3π,logπ3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+a2.
(I)若f(x)在x=1处有极值10,求a,b的值;
(II)若当a=-1时,f(x)<0在x∈[1,2]恒成立,求b的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)(i)利用(1)所求的回归方程,预测该市车流量为8万辆时![]() 的浓度;
的浓度;
(ii)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
参考公式:回归直线的方程是![]() ,其中
,其中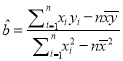 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=
的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=![]() ,
,
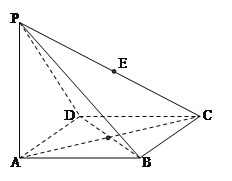
(1)求证:平面PBD⊥平面PAC;
(2)求三棱锥P--BDC的体积。
(3)在线段PC上是否存在一点E,使PC⊥平面EBD成立.如果存在,求出EC的长;如果不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com