Question

时值5月，荔枝上市．某市水果市场由历年的市场行情得知，从5月10日起的60天内，荔枝的售价S（t）（单位：元/kg）与上市时间t（单位：天）的关系大致可用如图1所示的折线ABCD表示，每天的销售量M（t）（单位：吨）与上市时间t（单位：天）的关系大致可用如图2所示的抛物线段OEF表示，其中O为坐标原点，E是抛物线的顶点．
（1）请分别写出S（t），M（t）关于t的函数关系式；
（2）在这60天内，该水果市场哪天的销售额最大？

Answer 1

分析：（1）根据图1，发现当0≤t≤10时，函数S（t）=10，而当10＜t≤40时和当40＜t≤60时，函数S（t）的表达式都是一次函数，可以先设出它们的一次解析式，利用图象上的已知点求出一次项系数和常数项，可以得到函数S（t）的函数关系式．对于M（t），根据它的图象是开口向下的抛物线，经过原点且关于直线t=40对称，结合顶点坐标，不难用待定系数的方法求出M（t）关于t的函数关系式；
（2）根据（1）的函数S（t）的分段函数关系式，分①当0≤t≤10时，②当10＜t≤40时，③当40＜t≤60时，分别得到P（t）关于t的函数关系式，利用导数工具讨论各段上的单调性，从而得出函数P（t）在各段上的最大值，再将各个最大值进行比较，从而得出当t=47时，水果市场的销售额最大．

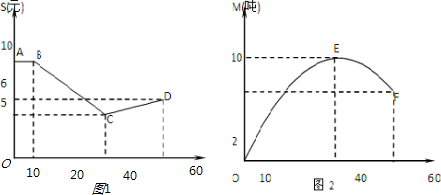
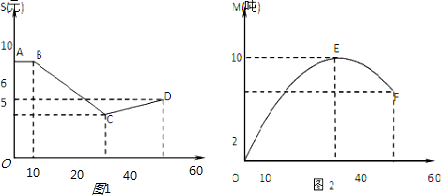
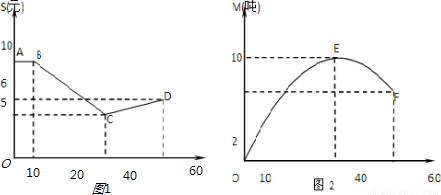
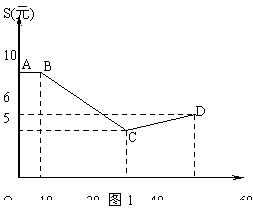
解答：解：（1）①由图1可知，当0≤t≤10时，S（t）=10
②当10＜t≤40时，设S（t）=a₁t+b₁，因为函数S（t）的图象过点B（10，10），C（40，5）
所以

10a1+b1=10 40a1+b1=5

，解之得

a 1=-  1 6 b 1=  35 3

∴当10＜t≤40时，S（t）=-

1

6

t+

35

3

③当40＜t≤60时，设S（t）=a₂t+b₂，因为函数S（t）的图象过点C（40，5），C（60，6），
所以用类似②的方法可得

a 2= 1 20 b 2 = 3

，此时S（t）=

1

20

t+3，
综上所述，S（t）=

10，   0≤t≤10，t∈N - 1 6 t+ 35 3 ，    10＜t≤40，t∈N 1 20 t+3，      40＜t≤60，t∈N

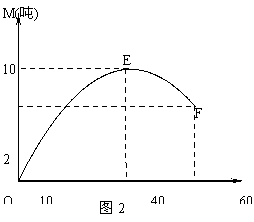
由图2可知，函数M（t）在x=40时取得最大值，故设M（t）=a（t-40）²+10
又函数M（t）的图象过点O（0，0），所以a（-40）²+10=0，解之得a=-

1

160

所以M（t）=-

1

160

（t-40）²+10=-

1

160

t²+

1

2

t，0≤t≤160，t∈N
（2）在这60天内，设该水果市场的销售额与天天数的函数关系为P（t），则
①当0≤t≤10，t∈N时，P（t）=1000S（t）M（t）=10000（-

1

160

t²+

1

2

t）
可得：当t=10时，P（t）_max=P（10）=43750．
②当10＜t≤40，t∈N时，P（t）=1000S（t）M（t）=1000（-

1

6

t+

35

3

）（-

1

160

t²+

1

2

t）=

25

24

（t³-150t²+5600t）
∵（t³-150t²+5600t）′=3t²-300t+5600=3（t-50）²-1900＞0在区间（10，24]上成立，
且（t³-150t²+5600t）′=3t²-300t+5600=3（t-50）²-1900＜0在区间[25，40]上成立
∴P（t）在区间（10，24]上是单调增函数，在区间[25，40]上是单调减函数
当10＜t≤40，t∈N时，P（t）_max应该是P（24）和P（25）中的较大者
而P（24）=64400，P（25）≈64453.13，因此P（t）_max=P（25）
③当40＜t≤60，t∈N时，P（t）=1000S（t）M（t）=1000（

1

20

t+3）（-

1

160

t²+

1

2

t）=

5

16

（-t³+20t²+4800t）
用类似②的方法，可得P（t）在区间（40，47]上是单调增函数，在区间[48，60]上是单调减函数．
而P（47）≈51861.56＞P（48）=51840，所以此时P（t）_max=P（47）
综上所述，P（t）的最大值为P（47）≈51861.56
所以在这60天内，该水果市场第47天的销售额最大．

点评：本题以一个实际问题为例，考查了分段函数的单调性与最值的知识点，计算量很大，是一道难题．在解题过程中用到了分类讨论与转化化归的思想，综合了函数多种性质加以解决．