
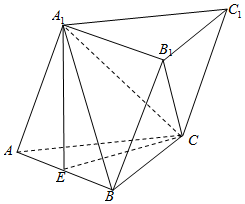
 在斜三棱柱ABC-A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.
在斜三棱柱ABC-A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.分析 (Ⅰ)根据线面平行的判定定理进行证明即可.
(Ⅱ)根据点到平面的距离公式以及线面角的定义,结合三角形的边角关系进行求解.
解答 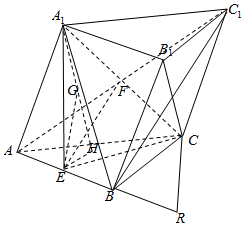 解:(I)证明:设AC1与A1C交于F点,连接EF,
解:(I)证明:设AC1与A1C交于F点,连接EF,
∵E,F分别是线段AB,AC1的中点,
∴EF∥BC1,又EF?平面 A1EC,BC1?平面A1EC
故 BC1∥平面A1EC,
(II)①在正三角形A BC中,过E作E H⊥AC于H,连接A1H
显然AC⊥平面A1EH,
∵AC?平面ACC1A1
∴平面A1EH⊥平面ACC1A1,且两个平面的交线为A1H
过E作EG⊥A1H于G,则EG⊥平面ACC1A1
在Rt△AA1B中,由已知易得A1E=1,在正三角形ABC中,${E}{H}=\frac{{\sqrt{3}}}{2}$
则在Rt△A1E H中,${E}G=\frac{{{{A}_1}{E}•{E}{H}}}{{\sqrt{{{A}_1}{{E}^2}+{E}{{H}^2}}}}=\frac{{\sqrt{21}}}{7}$
即点E到平面ACC1A1的距离为$\frac{{\sqrt{21}}}{7}$,
∵E是线段AB中点,
∴点B到平面ACC1A1的距离$d=2{E}G=\frac{{2\sqrt{21}}}{7}$,
②延长EB至R点,使EB=BR=1,连接RC,
∴B1R∥A1E,则B1R⊥平面ARC,即有B1R⊥RC
在△BRC中易得$RC=\sqrt{7}$,
∴${{B}_1}C=2\sqrt{2}$
设直线B1C与平面ACC1A1所成角为φ
则$sinφ=\frac{d}{{{{B}_1}C}}=\frac{{\sqrt{42}}}{14}$.
点评 本题考查直线平行的证明,考查点到平面的距离以及线面角的求法,利用相应的判定定理以及线面角的定义进行求解是解决本题的关键.考查学生的运算和推理能力.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在斜三棱柱ABC-A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.
在斜三棱柱ABC-A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 5 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com