
【题目】如图,在四棱锥PABCD中,M是PA上的点,![]() 为正三角形,
为正三角形,![]() ,
,![]() .
.
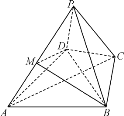
(1)求证:平面![]() 平面PAC;
平面PAC;
(2)若![]() ,
,![]() 平面BPC,求证:点M为线段PA的中点.
平面BPC,求证:点M为线段PA的中点.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)取BD的中点O,连结OA,OC,可证![]() ,又由
,又由![]() ,可得
,可得![]() 平面PAC,即可得证;
平面PAC,即可得证;
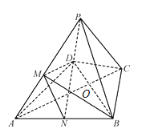
(2)取AB的中点N,连结MN和DN,首先可得![]() ,
,![]() ,所以
,所以![]() ,即可得到
,即可得到![]() 平面BPC.又由
平面BPC.又由![]() 平面BPC,可得平面
平面BPC,可得平面![]() 平面BPC.根据面面平行的性质可得
平面BPC.根据面面平行的性质可得![]() ,即可得证;
,即可得证;
(1)取BD的中点O,连结OA,OC,
∵![]() 为正三角形,∴
为正三角形,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
在平面![]() 内,过O点垂直于BD的直线有且只有一条,
内,过O点垂直于BD的直线有且只有一条,
∴A,O,C三点共线,即![]() .
.
∵![]() ,AC,
,AC,![]() 平面PAC,
平面PAC,![]() ,
,
∴![]() 平面PAC.∵
平面PAC.∵![]() 平面MBD,
平面MBD,
∴平面![]() 平面PAC.
平面PAC.
(2)取AB的中点N,连结MN和DN,
因为![]() ,且
,且![]() ,所以
,所以![]()
所以![]() ,即
,即![]() .
.
∵![]() 为正三角形,∴
为正三角形,∴![]() .
.
又DN,BC,AB共面,∴![]() .
.
∵![]() 平面BPC,
平面BPC,![]() 平面BPC,
平面BPC,
∴![]() 平面BPC.
平面BPC.
∵![]() 平面BPC,DN,
平面BPC,DN,![]() 平面DMN,
平面DMN,
∴平面![]() 平面BPC.
平面BPC.
∵![]() 平面DMN,∴
平面DMN,∴![]() 平面BPC.
平面BPC.
∵![]() 平面PAB,平面
平面PAB,平面![]() 平面BPC=PB,
平面BPC=PB,
∴![]() .
.
∵N是AB的中点,∴M为线段PA的中点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列4个说法中正确的有( )
①命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() 则
则![]() ”;
”;
②若![]() ,则
,则![]() ;
;
③若复合命题:“![]() ”为假命题,则p,q均为假命题;
”为假命题,则p,q均为假命题;
④“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A.①②③B.②③④C.①②④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,
为等差数列,![]() ,
,![]() ,
,![]() 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且![]() ,
,![]() ,
,![]() 中的任何两个数都不在下表的同一列.
中的任何两个数都不在下表的同一列.
第一列 | 第二列 | 第三列 | |
第一行 | |||
第二行 | 4 | 6 | 9 |
第三行 | 12 | 8 | 7 |
请从①![]() ,②
,②![]() ,③
,③ ![]() 的三个条件中选一个填入上表,使满足以上条件的数列
的三个条件中选一个填入上表,使满足以上条件的数列![]() 存在;并在此存在的数列
存在;并在此存在的数列![]() 中,试解答下列两个问题
中,试解答下列两个问题
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校实行新课程改革,即除语、数、外三科为必考科目外,还要在理、化、生、史、地、政六科中选择三科作为选考科目.已知某生的高考志愿为某大学环境科学专业,按照该大学上一年高考招生选考科目要求理、化必选,为该生安排课表(上午四节、下午四节,每门课每天至少一节),已知该生某天最后两节为自习课,且数学不排下午第一节,语文、外语不相邻(上午第四节和下午第一节不算相邻),则该生该天课表有( ).
A.444种B.1776种C.1440种D.1560种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,抛物线上的点
,抛物线上的点![]() 到焦点的距离为2.
到焦点的距离为2.
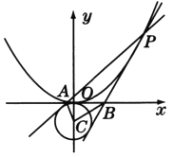
(1)求抛物线的方程和![]() 的值;
的值;
(2)如图,![]() 是抛物线上的一点,过
是抛物线上的一点,过![]() 作圆
作圆![]() 的两条切线交
的两条切线交![]() 轴于
轴于![]() ,
,![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com