
已知 为椭圆
为椭圆
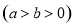 的左右焦点,
的左右焦点, 是坐标原点,过
是坐标原点,过 作垂直于
作垂直于 轴的直线
轴的直线 交椭圆于
交椭圆于 ,设
,设 .
.
(1)证明: 成等比数列;
成等比数列;
(2)若 的坐标为
的坐标为 ,求椭圆
,求椭圆 的方程;
的方程;
(3)在(2)的椭圆中,过 的直线
的直线 与椭圆
与椭圆 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.
(1)详见解析;(2)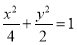 ;(3)
;(3)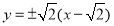
【解析】
试题分析:(1)由条件知M点的坐标为(c,y0),其中|y0|=d,知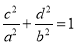 ,d=b•
,d=b•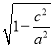 =
=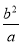 ,由此能证明d,b,a成等比数列.
,由此能证明d,b,a成等比数列.
(2)由条件知c=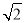 ,d=1,知b2=a?1,a2=b2+2,由此能求出椭圆方程.
,d=1,知b2=a?1,a2=b2+2,由此能求出椭圆方程.
(3)设点A(x1,y1)、B(x2,y2),当l⊥x轴时,A(-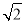 ,-1)、B(-
,-1)、B(-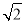 ,1),所以
,1),所以 ≠0. 设直线
≠0. 设直线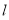 的方程为y=k(x+
的方程为y=k(x+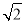 ),代入椭圆方程得(1+2k2)x2+4
),代入椭圆方程得(1+2k2)x2+4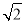 k2x+4k2?4=0再由韦达定理能够推导出直线
k2x+4k2?4=0再由韦达定理能够推导出直线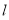 的方程.
的方程.
试题解析:(1)证明:由条件知M点的坐标为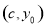 ,其中
,其中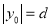 ,
,
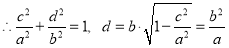 ,
, 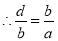 ,即
,即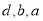 成等比数列. 3分
成等比数列. 3分
(2)由条件知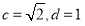 ,
,
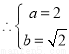
 椭圆方程为
椭圆方程为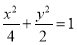 6分
6分
(3)设点A(x1,y1)、B(x2,y2),当l⊥x轴时,A(-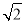 ,-1)、B(-
,-1)、B(-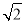 ,1),所以
,1),所以 ≠0. 设直线
≠0. 设直线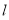 的方程为y=k(x+
的方程为y=k(x+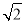 ),代入椭圆方程得(1+2k2)x2+4
),代入椭圆方程得(1+2k2)x2+4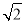 k2x+4k2?4=0所以
k2x+4k2?4=0所以 ①由
①由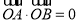 得
得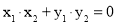
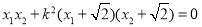 整理后把①式代入解得k=
整理后把①式代入解得k=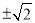 ,
,
所以直线l的方程为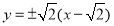 .
.
考点:数列与解析几何的综合.


科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试理数学试卷(解析版) 题型:选择题
用辗转相除法求294和84的最大公约数时,需要做除法的次数是
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源:2015届云南玉溪一中高二上学期期末考试文科数学试卷(解析版) 题型:选择题
已知函数 的周期为2,当
的周期为2,当 ,如果
,如果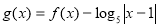 ,则函数
,则函数 的所有零点之和为( )
的所有零点之和为( )
A.2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习真题感悟常考问题7练习卷(解析版) 题型:填空题
如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=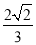 ,AB=3
,AB=3 ,AD=3,则BD的长为______.
,AD=3,则BD的长为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com