
【题目】下列四个命题,其中m,n,l为直线,α,β为平面
①mα,nα,m∥β,n∥βα∥β;
②设l是平面α内任意一条直线,且l∥βα∥β;
③若α∥β,mα,nβm∥n;
④若α∥β,mαm∥β.
其中正确的是( )
A.①②
B.②③
C.②④
D.①②④
【答案】C
【解析】解:在长方体ABCD﹣A1B1C1D1中,
①若平面AC是平面α,平面A1C1是平面β,
直线AD是直线m,A1B1是直线n,
显然满足mα,nα,m∥β,n∥β,但是α与β相交,不正确;
②若平面α内任意一条直线平行于平面β,则平面α的两条相交直线平行于平面β,满足面面平行的判定定理,所以α∥β;故正确
③若平面AC是平面α,平面BC1是平面β,
直线AD是直线m,点E,F分别是AB,CD的中点,则EF∥AD,EF是直线n,
显然满足α∥β,mα,nβ,但是m与n异面,不正确;
④由面面平行结合线面平行的定义可得m∥β,正确,
故选:C.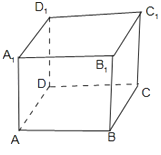
【考点精析】利用空间中直线与平面之间的位置关系对题目进行判断即可得到答案,需要熟知直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘车补贴标准如下表:

某校研究性学习小组,从汽车市场上随机选取了![]() 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程![]() (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:

(1)求![]() 的值;
的值;
(2)若从这![]() 辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为![]() (单位:万元),求
(单位:万元),求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为 (为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线
(为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若![]() 与
与![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE= ![]() ,且当规定正视图方向垂直平面ABCD时,该几何体的侧视图的面积为
,且当规定正视图方向垂直平面ABCD时,该几何体的侧视图的面积为 ![]() .若M,N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为
.若M,N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为 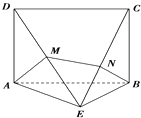
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,且f(x)不为常值函数,有以下命题:
①函数g(x)=f(x)+f(﹣x)一定是偶函数;
②若对任意x∈R都有f(x)+f(2﹣x)=0,则f(x)是以2为周期的周期函数;
③若f(x)是奇函数,且对于任意x∈R,都有f(x)+f(2+x)=0,则f(x)的图象的对称轴方程为x=2n+1(n∈Z);
④对于任意的x1 , x2∈R,且x1≠x2 , 若![]() >0恒成立,则f(x)为R上的增函数,
>0恒成立,则f(x)为R上的增函数,
其中所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有这样一则问题:“今有良马与弩马发长安,至齐,齐去长安三千里,良马初日行一百九十三里,日增一十三里;弩马初日行九十七里,日减半里,良马先至齐,复还迎弩马.”则现有如下说法:
①弩马第九日走了九十三里路;
②良马前五日共走了一千零九十五里路;
③良马和弩马相遇时,良马走了二十一日.
则以上说法错误的个数是( )个
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且f(x)在(﹣∞,0]上单调递减,则不等式f(lgx)>f(﹣2)的解集是( )
A.( ![]() ,100)
,100)
B.(100,+∞)
C.( ![]() ,+∞)
,+∞)
D.(0, ![]() )∪(100,+∞)
)∪(100,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线![]() .根据图中数据,下列对该样本描述错误的是( )
.根据图中数据,下列对该样本描述错误的是( )
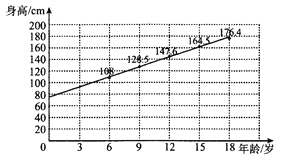
A. 据样本数据估计,该地区青少年身高与年龄成正相关
B. 所抽取数据中,5000名青少年平均身高约为![]()
C. 直线![]() 的斜率的值近似等于样本中青少年平均身高每年的增量
的斜率的值近似等于样本中青少年平均身高每年的增量
D. 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线![]() 上
上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com