考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)化约束条件为不等式组,进而作出其对应的平面区域,变形目标函数经平移直线得最优解,代值得答案.
(2)z表示正方形及其内部的点(x,y)到(2,-2)的距离的平方减去8.求得正方形位于第四象限的边所在的直线方程为x-y-1=0,以及点(2,-2)到此直线的距离d的值,可得z=x
2+y
2-4x+4y的最小值.
(3)z=2•
,表示正方形及其内部的点(x,y)与点M(5,-
)连线的斜率的2倍.显然点N(0,-1)与点M(5,-
)连线的斜率最大,求得此最大值,再乘以2,即为所求.
解答:
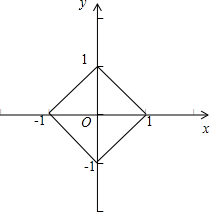
解:(1)约束条件|x|+|y|≤1可化为:
| | x+y≤1,x≥0,y≥0 | | x-y,x≥0,y<0 | | -x+y,x<0,y≥0 | | -x-y,x<0,y<0 |
| |
,
其表示的平面区域如图所示的正方形及内部:
设目标函数z=x+2y,变形可得y=-
x+
,
经平移直线可知当直线经过点(0,1)时,z=x+2y取最大值2.
(2)z=x
2+y
2-4x+4y=(x-2)
2+(y+2)
2-8,表示正方形及其内部的点(x,y)到(2,-2)的距离的平方减去8.
正方形位于第四象限的边所在的直线方程为x-y-1=0,求得点(2,-2)到此直线的距离为d=
=
,
可得z=x
2+y
2-4x+4y的最小值为
-8=-
.
(3)z=
=2
,表示正方形及其内部的点(x,y)与点M(5,-
)连线的斜率的2倍.
显然点N(0,-1)与点M(5,-
)连线的斜率最大为
=
,
故z=
的最大值为2×
=
.
点评:本题考查简单线性规划,两点间的距离公式、直线的斜率公式的应用,画出满足条件的可行域,确定最优解是解决问题的关键,属中档题.

 解:(1)约束条件|x|+|y|≤1可化为:
解:(1)约束条件|x|+|y|≤1可化为:

 阅读快车系列答案
阅读快车系列答案