
分析 (Ⅰ)抛物线的准线方程为l′:x=-$\frac{p}{2}$,推出△MNF为等边三角形,进而得到抛物线方程;
(Ⅱ)设直线l的方程为y=k(x-1),联立抛物线方程运用韦达定理,代入所求式子化简即可得到定值-1
解答  解:(Ⅰ)抛物线的准线方程为l′:x=-$\frac{p}{2}$,过点M作MN⊥l′交于点N,连接NF,
解:(Ⅰ)抛物线的准线方程为l′:x=-$\frac{p}{2}$,过点M作MN⊥l′交于点N,连接NF,
由抛物线的定义可知|MN|=|FM|,
又∠NMF=∠MFx=60°,
所以△MNF为等边三角形,
所以|NF|=4,于是p=2,
所以抛物线的方程为y2=4x,
(Ⅱ)设直线l的方程为y=k(x-1),
联立y2=4x,消去y可得k2x2-(2k2+4)+k2=0,
因为A(x1,y1),B(x2,y2),
则x1x2=1,x1+x2=$\frac{2{k}^{2}+4}{{k}^{2}}$=2+$\frac{4}{{k}^{2}}$
又$\frac{|PA|}{|AF|}$=$\frac{{x}_{1}}{1-{x}_{1}}$,$\frac{|PB|}{|BF|}$=$\frac{{x}_{2}}{{x}_{2}-1}$,
所以$\frac{|PA|}{|AF|}$-$\frac{|PB|}{|BF|}$=$\frac{{x}_{1}}{1-{x}_{1}}$-$\frac{{x}_{2}}{{x}_{2}-1}$=$\frac{2{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})}{({x}_{1}+{x}_{2})-1-{x}_{1}{x}_{2}}$=$\frac{2-2-\frac{4}{{k}^{2}}}{2+\frac{4}{{k}^{2}}-1-1}$=-1,
即$\frac{|PA|}{|AF|}$-$\frac{|PB|}{|BF|}$为定值,且定值为-1.
点评 本题考查抛物线的方程和性质,考查直线方程和抛物线方程联立,运用韦达定理,考查运算能力,属于中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
 将某选手的9个得分去掉一个最高分,去掉一个最低分,7个剩余分数的平均分为91,现场作的9个得分的茎叶图,后来有一个数据模糊,无法辨认,在图中以x表示,则x为4.
将某选手的9个得分去掉一个最高分,去掉一个最低分,7个剩余分数的平均分为91,现场作的9个得分的茎叶图,后来有一个数据模糊,无法辨认,在图中以x表示,则x为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 1+$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
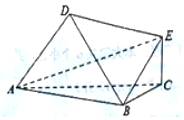 如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2.
如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com