
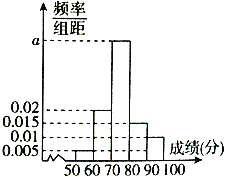
����Ŀ��Ϊ���˽�ijѧУ�߶��꼶ѧ���������ɼ������г�ȡn��ѧ���������ɼ����ٷ��ƣ���Ϊ���������ɼ��ֳ� 5�飺[50��60����[60��70����[70��80����[80��90����[90��100]��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���ɼ�����[70��80���е�����Ϊ20��
���� | Ů�� | �ϼ� | |
���� | |||
������ | |||
�ϼ� |
������a��n��ֵ��
�������������������˼�룬���Ƹ�У�߶�ѧ�������ɼ���ƽ����![]() ����λ��m��
�����m��
���ɼ���80�����ϣ���80�֣�Ϊ���㣬�����гɼ�����[50��80���е��С�Ů��������Ϊ1��2���ɼ�����[80��100]�е��С�Ů��������Ϊ3��2�����2��2�����������ж��Ƿ���95%�İ�����Ϊ�����ɼ��������Ա��йأ�
�ο���ʽ�����ݣ�K2=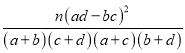 ��
��
P��K2��k�� | 0.50 | 0.05 | 0.025 | 0.005 |
k | 0.455 | 3.841 | 5.024 | 7.879 |
���𰸡���1��a=0.05,n=40��2��m=75��3��û��95%�İ�����Ϊ�����ɼ��������Ա��й�
�������������������1������С�����ε������Ϊ1���![]() ��Ȼ�����
��Ȼ�����![]() ��n����2�����ø�����м�ֵ��Ƶ�ʵij˻�����ƽ������������λ����Ƶ�ʷֲ�ֱ��ͼ��Ϊ�����ȵ�����������λ������3����������д�����������ݹ�ʽ���K2,���òο����ݽ����жϡ�
��n����2�����ø�����м�ֵ��Ƶ�ʵij˻�����ƽ������������λ����Ƶ�ʷֲ�ֱ��ͼ��Ϊ�����ȵ�����������λ������3����������д�����������ݹ�ʽ���K2,���òο����ݽ����жϡ�
���������
����������ɵ�
10a=1����0.005+0.01+0.015+0.02����10��
��a=0.05��
�� n=![]() =40
=40
���������⣬�����Ƶ�ʷֱ�Ϊ0.05��0.2��0.5��0.15��0.1��
��![]() =55��0.05+65��0.2+75��0.5+85��0.15+95��0.1=75.5��
=55��0.05+65��0.2+75��0.5+85��0.15+95��0.1=75.5��
����λ��Ϊm��
��m��70����0.05=0.5����0.05+0.2����
��m=75��
���������⣬���������Ϊ6�ˣ�Ů��Ϊ4�ˣ������������Ϊ10�ˣ�Ů��Ϊ20�ˣ�
2��2������
���� | Ů�� | �ϼ� | |
���� | 6 | 4 | 10 |
������ | 10 | 20 | 30 |
�ϼ� | 16 | 24 | 40 |
�ɱ��ɵ�
K2=![]() ��2.222��3.841��
��2.222��3.841��
��û��95%�İ�����Ϊ�����ɼ��������Ա��йأ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
��
��I�� ���ۺ���![]() �ĵ������䣻
�ĵ������䣻
��II����![]() ʱ��������
ʱ��������![]() ������
������![]() �ϵ����ֵΪ3����
�ϵ����ֵΪ3����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}�У�a1=1��an+1=an+2n+1��������{bn}����bn=an��1��������������n����ʽ ![]() ����������ʵ��m��ȡֵ��ΧΪ ��
����������ʵ��m��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABC��A1B1C1�У�AC��BC����D��AB���е㣮��֤�� 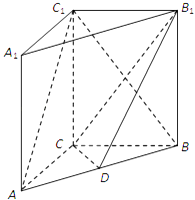
��1��AC��BC1��
��2��AC1��ƽ��B1CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P��ABCD�У���PABΪ�������Σ��ı���ABCDΪ���Σ�ƽ��PAB��ƽ��ABCD��AB=2AD��M��N�ֱ�ΪPB��PC�е㣮
������֤��MN��ƽ��PAD��
����������B��AM��C�Ĵ�С��
������BC���Ƿ���ڵ�E��ʹ��EN��ƽ��AMN�������ڣ��� ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ͼ���ԭ��,����
��ͼ���ԭ��,����![]() ��ȡ�ü�ֵ,ֱ��
��ȡ�ü�ֵ,ֱ��![]() ������
������![]() ��ԭ�㴦�������ഹֱ.
��ԭ�㴦�������ഹֱ.
����������![]() �Ľ���ʽ��
�Ľ���ʽ��
��������������ʵ����![]() ,����
,����![]() ����,��ʵ��
����,��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
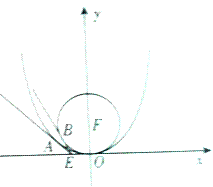
����Ŀ����ͼ��ʾ��������C��x2=2py��p��0�����佹��ΪF��C�ϵ�һ��M��4��m������|MF|=4��
��1����������C�ı����̣�
��2������E����1��0����������ԭ�������ֱ��EA��EB�ֱ���������C��ԲF��x2+��y��2��2=4�����ڵ�A��B�����ж�ֱ��AB�Ƿ�����F��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ3��������![]() ����ƽ�������ֱ��������
����ƽ�������ֱ��������![]() ����ƽ�滥�ഹֱ��
����ƽ�滥�ഹֱ�� ![]() ����
����![]() ��
�� ![]() .
.
������֤�� ![]() ƽ��
ƽ��![]() ��
��
����������![]() ������ֵ.
������ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l����P��3��6������x��y���������ֱ���A��B���㣬O������ԭ�㣬��|OA|+|OB|ȡ����Сֵʱ��ֱ�߷���������һ��ʽ��ʾ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com