
如下图,两条异面直线AB、CD与三平行平面α、β、γ分别相交于A、E、B及C、F、D,又AD、BC与平面β的交点为H、G,求证:四边形EHFG为平行四边形.
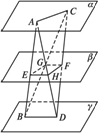
科目:高中数学 来源:湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型:047
如下图,两条异面直线AB、CD与三个平行平面α、β、?分别相交于A、E、B,及C、F、D,又AD、BC与平面β的交点为H、G.求证:EHFG为平行四边形.
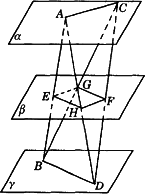
查看答案和解析>>
科目:高中数学 来源: 题型:013
(1)
如下图是正方体的平面展开图,则在这个正方体中:|
① 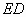 平行. 平行. |
② 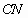 与 与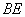 是异面直线. 是异面直线. |
|
③ 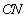 与 与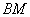 成60°角. 成60°角. |
④  与 与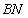 是异面直线. 是异面直线. |
以上四个命题中,正确命题的序号是
[
]|
(A) ①②③ |
(B) ②④ |
|
(C) ③④ |
(D) ②③④ |

(2)
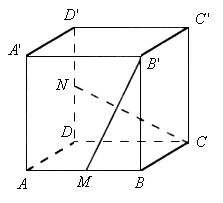
如下图,正方体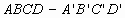 中,
中,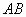 的中点为
的中点为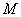 ,
,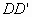 的中点为
的中点为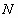 ,则异面直线
,则异面直线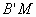 与
与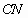 所成的角是
所成的角是
[
]|
(A)0° |
(B)45° |
(C)60° |
(D)90° |
(3)
给出三个命题:①若两条直线和第三条直线所成的角相等,则这两条直线互相平行.
②若两条直线都与第三条直线垂直,则这两条直线互相平行.
③若两条直线都与第三条直线平行,则这两条直线互相平行.
其中不正确命题的个数是
[
]|
(A)0 |
(B)1 |
(C)2 |
(D)3 |
查看答案和解析>>
科目:高中数学 来源: 题型:022
(1)
已知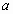 ,
,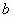 ,
,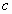 是三条直线,且
是三条直线,且 ∥
∥ ,
,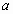 与
与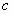 的夹角为
的夹角为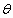 ,那么
,那么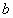 与
与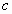 夹角为______;
夹角为______;
(2)
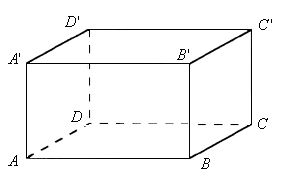
如下图, 是长方体的一条棱,这个长方体中与
是长方体的一条棱,这个长方体中与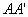 垂直的棱共______条;
垂直的棱共______条;
(3)
如果 ,
,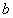 是异面直线,直线
是异面直线,直线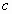 与
与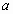 ,
,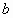 都相交,那么这三条直线中的两条所确定的平面共有_______个;
都相交,那么这三条直线中的两条所确定的平面共有_______个;
(4)
若一条直线与两个平行平面中的一个平面平行,则这条直线与另一个平面的位置关系是______;(5)
已知两条相交直线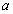 ,
,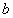 ,
,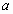 ∥平面
∥平面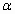 ,则
,则 与
与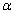 的位置关系是______;
的位置关系是______;
(6)设直线
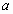 ,
,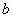 分别是长方体相邻两个面的对角线所在的直线,则
分别是长方体相邻两个面的对角线所在的直线,则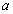 与
与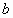 的位置关系是______.
的位置关系是______.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com