Question

【题目】如图，在四棱锥S﹣ABCD中，底面ABCD是直角梯形，侧棱SA⊥底面ABCD，AB垂直于AD和BC，SA=AB=BC=2，AD=1．M是棱SB的中点．
（Ⅰ）求证：AM∥面SCD；
（Ⅱ）求面SCD与面SAB所成二面角的余弦值；
（Ⅲ）设点N是直线CD上的动点，MN与面SAB所成的角为θ，求sinθ的最大值．

Answer 1

【答案】解：（Ⅰ）以点A为原点建立如图所示的空间直角坐标系，

则A（0，0，0），B（0，2，0），D（1，0，0，），S（0，0，2），M（0，1，1）．
则 ， ， ．
设平面SCD的法向量是 ，则 ，即
令z=1，则x=2，y=﹣1．于是 ．
∵ ，∴ ．
又∵AM平面SCD，∴AM∥平面SCD．
（Ⅱ）易知平面SAB的法向量为 ．设平面SCD与平面SAB所成的二面角为α，
则 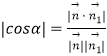= = ，即 ．
∴平面SCD与平面SAB所成二面角的余弦值为 ．
（Ⅲ）设N（x，2x﹣2，0），则 ．
∴ = = = ．
当 ，即 时， ．
【解析】（Ⅰ）通过建立空间直角坐标系，利用平面SCD的法向量 即可证明AM∥平面SCD；（Ⅱ）分别求出平面SCD与平面SAB的法向量，利用法向量的夹角即可得出；（Ⅲ）利用线面角的夹角公式即可得出表达式，进而利用二次函数的单调性即可得出．